C# – Verificando se um número é primo

Hoje veremos algumas abordagens que podemos usar para verificar se um número é primo usando a linguagem C#. Um inteiro maior do que 1 é chamado de número primo se seus únicos divisores positivos (fatores) forem o número 1 e ele mesmo.

Por exemplo, os divisores primos de 10 são 2 e 5; e os primeiros seis números primos são 2, 3, 5, 7, 11 e 13. O número 1 não é primo e o número 2 é o único número primo par.

Assim, se n (n > 1) é um número inteiro.

Dizemos que:

n é primo se os únicos divisores positivos de n são 1 e n.
n é composto se n não é primo. (3) = {1, 3}.

Para testar se um dado número é primo podemos usar um código bem simples como o abaixo onde usamos um laço for/next :

Console.WriteLine(“### Verificando se um número é primo ###\n”);while(true)
{
Console.WriteLine(“Informe um número até 99998 (99999 sai)”);
var numero = Int32.Parse(Console.ReadLine());

if (numero == 99999)
break;

if (numero < 2 || numero > 99998)
{
Console.WriteLine(“Número menor que 2 e maior
que 1000 não vale”);
}
else
{
var resultado = VerificaNumeroPrimo(numero);
Console.WriteLine(“O número {0} {1} primo.\n”,
numero, resultado ? “É” : “NÃO “);
}
}

bool VerificaNumeroPrimo(int numero)
{
bool ePrimo = true;
for (int divisor = 2; divisor <= Math.Sqrt(numero); divisor++)
{
if (numero % divisor == 0)
{
ePrimo = false;
break;
}
}
return ePrimo;
}

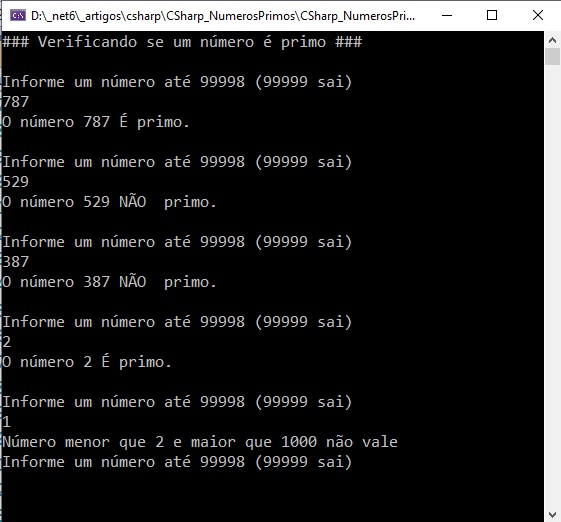
Abaixo temos o projeto em execução:

Usando LINQ podemos otimizar o código e obter o mesmo resultado, para isso basta criar o método VerificaNumeroPrimoLINQ(int numero) com o código a seguir:

bool VerificaNumeroPrimoLINQ(int numero)
{
bool ePrimo = Enumerable.Range(2, (int)Math.Sqrt(numero) – 1)
.All(divisor => numero % divisor != 0);

return ePrimo;
}

Usando outra abordagem

Aqui está um código alternativo e mais enxuto para verificar se um número é primo em C#:

public static bool IsPrime(int numero)
{
if (numero <= 1)
{
return false;
}

for (int i = 2; i <= Math.Sqrt(numero); i++)
{
if (numero % i == 0)
{
return false;
}
}

return true;
}

Este código é otimizado porque verifica apenas os números até a raiz quadrada do número. Isso é porque se um número for divisível por qualquer número maior que sua raiz quadrada, ele também será divisível por todos os números menores que sua raiz quadrada.Este código também é robusto porque verifica se o número é menor ou igual a 1. Se o número for menor ou igual a 1, ele não é primo.

Você pode usar este código para verificar se qualquer número é primo. Por exemplo, para verificar se o número 13 é primo, você pode usar o seguinte código:

bool isPrime = IsPrime(13);

Implementando o Crivo de Eratóstenes

Outra abordagem é implementar o algoritmo de Crivo de Eratóstenes, que é um método eficiente para encontrar todos os números primos até um determinado valor.

using System;

class Program
{
static void Main()
{ // Altere o número que deseja verificar aqui
int numero = 37;

if (IsPrime(numero))
Console.WriteLine(#8221;{numero} é primo.”);
else
Console.WriteLine(#8221;{numero} não é primo.”);
}

static bool IsPrime(int numero)
{
if (numero<= 1)
return false;

if (numero<= 3)
return true;

if (numero% 2 == 0 || numero% 3 == 0)
return false;

int i = 5;
while (i * i <= numero)
{
if (numnumerober % i == 0 ||
numero% (i + 2) == 0)
return false;
i += 6;
}

return true;
}
}

Essa implementação é robusta e otimizada para verificar se um número é primo.

Ela evita iterações desnecessárias e é eficiente mesmo para números grandes. No entanto, é importante observar que a eficiência do algoritmo de Crivo de Eratóstenes diminui para números muito grandes, e nesses casos, podem ser necessários métodos mais avançados de teste de primalidade, como o teste deMiller-Rabin.

Pegue o projeto aqui: CSharp_NumerosPrimos.zip

*O conteúdo deste artigo é de responsabilidade do(a) autor(a) e não reflete necessariamente a opinião do iMasters.

De 0 a 10, o quanto você recomendaria este artigo para um amigo?

Powered by:

C# – Verificando se um número é primo

José Carlos Macoratti

José Carlos Macoratti