Esta será uma série sobre redes neurais artificiais, onde pretendo abordar desde a teoria, até a prática. Mas até chegarmos no código o caminho é longo – não estamos brincando com “Watson” aqui.

Se você está procurando entender, de fato, como funciona uma rede neural em seu nível roots (e de uma forma fácil também, né?) esta série é pra você!

Vou abordar desde o que é um neurônio (com Python e Go), até mesmo redes convolucionais mais famosas CNN (com o Tensorflow) e espero chegar, quem sabe, a explicar algumas coisas do estado da arte.

O que é uma Rede Neural Artificial?

Uma Rede Neural Artificial (RNA) é um modelo computacional que se inspira na forma como as redes neurais biológicas no cérebro humano processam informações.

Basicamente, é uma tentativa de replicar o comportamento dos neurônios do seu cérebro (um monte de neurônios se comunicando).

As Redes Neurais Artificiais geraram muito barulho no meio acadêmico e na indústria de Machine Learning (Machine learning não é só RNA), graças a muitos resultados inovadores em processamento de texto, visão computacional e reconhecimento de voz (acredito que nessa mesma ordem).

Neste artigo tentaremos desenvolver um entendimento de um tipo particular de Rede Neural Artificial, chamado Multi Layer Perceptron.

Como funciona um neurônio?

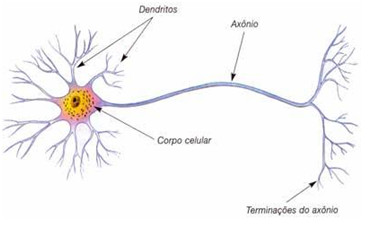
Os neurônios são compostos basicamente por três partes:

• 1 – Dentritos: resposáveis por captar informações
• 2 –  Corpo celular/Soma: responsáveis por processar as informações
• 3 – Axônio: responsável por distribuir as informações processadas para outros neurônios ou células do corpo

Uma célula dificilmente trabalha sozinha. Quanto mais células trabalharem em conjunto, mais informação elas podem processar, e mais eficaz se torna o trabalho. Logo, para o melhor rendimento do sistema são necessários muitos neurônios.

Eu sei que essa explicação não ajudou muito, pois muito provavelmente você que está lendo este artigo não deve ser nenhum neurologista (mas se for, comente ai em baixo).

Antes de começar a falar de neurônio, vamos falar de regressão

Primeiro, o objetivo da maioria dos algoritmos de Machine Learning é construir um modelo: uma hipótese que pode ser usada para estimar algo com base em um padrão.

A hipótese/predição/modelo, mapeia entradas para saídas. Por exemplo, digamos que eu treine um modelo baseado em um monte de dados de imobiliária que inclua o tamanho da casa e o preço de venda.

Ao treinar um modelo (achar os pesos corretos para nossos neurônios), posso fornecer uma estimativa de quanto você pode vender sua casa com base no tamanho dela. Este é um exemplo de um problema de regressão – dado algum input, queremos prever uma saída contínua.

Outro exemplo é em cima de problemas de time series, onde você tem registros de dois anos do preço de uma casa e quer prever o valor dessa mesma casa daqui a um ano, com base na valorização do imóvel dos últimos dois anos.

Caso queira algo mais visual ou um exemplo mais completo, assista o vídeo abaixo:

Para ilustrar um pouco a fórmula, teremos o valor atual da casa (bias) mais o valor de quanto essa casa se valoriza a cada mês (valor de a ou x, no caso no nosso neurônio. Relaxa, é só questão de nomenclatura) e o valor de quantos meses queremos predizer (valor de x ou w no caso dos neurônios).

No final, teremos a seguinte fórmula:

• (ValorizaçãoMensal*5meses+ValorAtualCasa) ou (a*x+b)

Como regressão linear não é o foco desta serie, sugiro que veja esse outro artigo sobre o tema, onde explico um pouco mais sobre o assunto.

Agora, o que é um Neurônio Artificial?

• Basicamente, é uma regressão múltipla.

A unidade mais básica de uma rede neural é um neurônio também conhecido como nó (caso você venha do mundo de grafos), tem apenas a capacidade de classificar sim ou não; é ou não é; isso é um cachorro ou não é um cachorro.

Essa classificação é dada a partir de uma regressão (ax+b) que recebe seus valores (de alguns outros neurônios ou de uma fonte externa, como um dataset, por exemplo) e calcula uma saída.

Cada entrada tem um peso associado (w), que é atribuído com base em sua importância (mas que não é você quem define isso – é definido no momento do aprendizado. Não se preocupe em saber como setar esse valor agora). O nó aplica uma função f (definida abaixo) à soma ponderada de suas entradas, conforme mostrado abaixo:

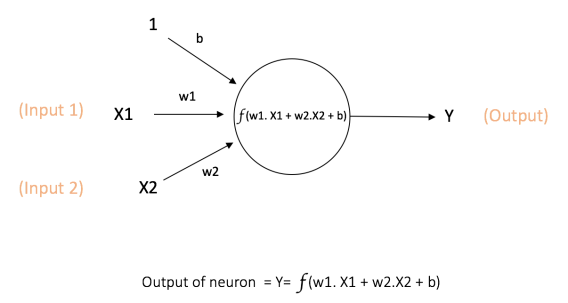
A fórmula ficou complicada. Deixe-me simplificar, então. Só pra ficar mais “ilustrativo/fácil” de entender o que cada valor significa, imagine que cada entrada (input1 e input2 na imagem acima) é o valor da cor RGB (0–255) de um pixel de uma imagem, e como essa imagem é composta por vários pixels, cada entrada tem o valor de 1 pixel, e o peso (peso representa a importância do pixel).

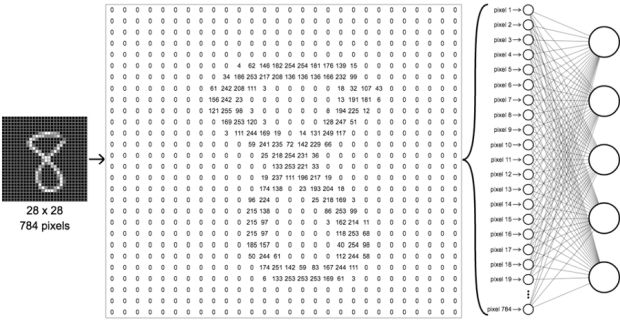
Você tem então suas entradas (duas entradas) e seus pesos (um peso para cada entrada). Imagine como se fossem quatro variáveis:

var x1,x2,w1,w2;

Aí você pega esse monte de variável, multiplica as entradas pelos pesos e depois soma tudo:

var result = (x1 * w1) + (x2 * w2)

Depois você adicionará uma constante chamada “bias” (pronuncia-se báias).

var y = result + b

Observação: esse “b” no meio da fórmula é uma constante. Caso esteja familiarizado com uma fórmula de uma função de primeiro grau, vai saber o que ele é (a.x+b).

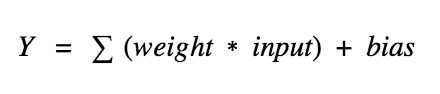
No final temos nosso resultado na variável y – essa é a nossa classificação do que estamos querendo classificar como sim ou não, seja lá o que for (essa imagem é de cachorro ou não é, essa imagem é gato ou não é? essa imagem é de fruta ou não é?).

Isso tudo é o que acontece dentro de um neurônio, e se você parar pra pensar, se você tiver um neurônio de uma entrada apenas, você terá a fórmula x1*w1+b, que é o mesmo que a*x+b.

Olha a matemática que você disse que nunca usaria (e essa é a matemática mais simples que você vai encontrar em redes neurais, aproveite!).

Agora, o valor de Y pode ser qualquer coisa entre valores positivos e negativos. Apenas a nossa função realmente não dá a informação de uma forma simples de interpretar ou até mesmo de mensurar se algo é ou não é o que estamos querendo classificar, então como decidimos se aquela imagem é ou não é sobre frutas?

Para isso podemos adicionar o que chamamos de “funções de ativação” para esse propósito. Para verificar o valor de Y produzido por um neurônio e decidir se as conexões externas devem considerar esse neurônio como “positivo” ou “negativo”, ou melhor, “ativado” ou não.

Uma função de ativação é basicamente uma fórmula que recebe um valor e que tem uma saída em uma escala binaria ou de 0 a 1 (0.0, 0.1, 0.2….0.9, 1.0).

Temos várias funções de ativação por ai – você escolherá a que faz mais sentido para a resolução do seu problema, mas não se preocupe, nesse momento você pode escolher qualquer uma – tanto faz a que você trabalhar, por enquanto.

Funções de ativação:

Step Function

A função mais simples que posso te apresentar neste momento é a step function, onde a regra é clara. Se a saída da sua função (lá de cima) for maior que zero, sua classificação é positiva. Caso contrário, é negativa.

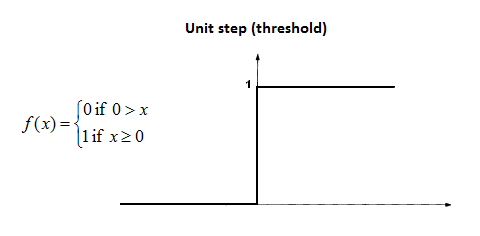
No caso dessa imagem, “X” equivale à nossa variável “y” lá em cima.

Isso faz com que eu tenha minha classificação usando apenas um neurônio. Bem simples, não é? No entanto, existem algumas desvantagens com isso.

Começando nossa rede neural

Esse não é o momento de começar a falar de rede neural, mas vou dar um leve briefing sobre o tema, apenas para poder dar continuidade ao assunto das funções de ativação.

Até então falamos de um neurônio, classificações binárias (é ou não é, sim ou não, 0 ou 1), mas agora queremos mais!

Queremos classificar três coisas – queremos identificar em uma foto se há uma criança, um adulto ou um idoso. Nesse caso, precisaremos de uma rede de neurônios. Vamos imaginar três neurônios por enquanto, onde o primeiro vai classificar se a foto tem ou não tem uma criança; o segundo vai classificar se a imagem tem ou não tem um adulto, e o terceiro neurônio vai dizer se há um idoso ou não.

Pelo o que você já viu até então, teremos três saídas. Caso tenhamos uma imagem classificada como “criança”, teremos a saída: criança=1,adulto=0,idoso=0 (1,0,0); se sair adulto, teremos criança=0,adulto=1,idoso=0 (0,1,0), e se tivermos idoso: criança=0,adulto=0,idoso=1 (0,0,1).

Mas e se mais de um neurônio for “ativado”? Todos os neurônios produzirão um 1 (da função step).

E se os neurônios de adulto e idoso forem ativados ao mesmo tempo? O que você decidiria? Que classe é essa?

Você gostaria que a rede ativasse apenas um neurônio e os outros deveriam ser 0 – somente então você seria capaz de dizer o que ele classifica.

Sendo assim, teria sido melhor se a ativação não fosse binária, e em vez disso dissesse uma probabilidade de algo ser ou não ser; de uma imagem ter ou não ter uma criança; ter ou não tem um adulto; ter ou não ter um idoso, e assim por diante.

Se mais de um neurônio for ativado, você poderá descobrir qual neurônio tem a “ativação mais alta”, e assim por diante.

Neste caso também, se mais de um neurônio disser “100% ativado”, o problema ainda persiste. Porém, uma vez que existem valores de ativação intermediários para a saída, as chances de mais de 1 neurônio ser 100% ativado são menores, se comparadas à função step.

Beleza, então queremos que algo forneça valores de ativação intermediários (analógicos) ao invés de dizer “ativado” ou não (binário).

Função Sigmoid

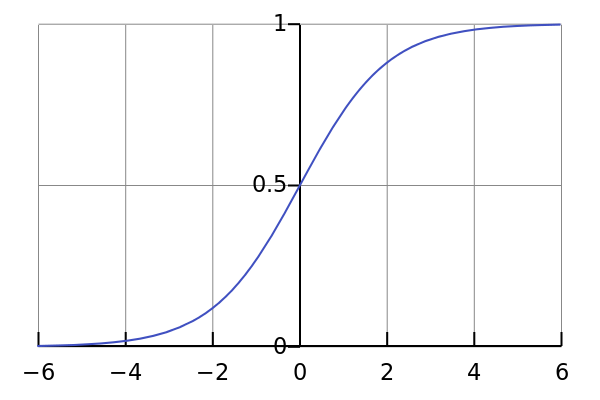
Lhes apresento a função Sigmoid (o nome “sigmóide” vem da forma em S do seu gráfico), e provavelmente vai ser a função que você vai mais usar nesse começo de carreira em redes neurais.

Calma, eu já vou mostrar como ela funcional. É uma fórmula – é só preencher as variáveis dela e ela faz toda a mágica (que nem em uma função do seu software).

Quais são os benefícios da Sigmoid?

A mágica está em sua natureza não linear, o que significa que ela não trabalha com uma reta em seu plano cartesiano. Simplificando: ela não trabalha só com 0 ou 1.

Ótimo, agora podemos trabalhar com nosso problema de classificação de faixa etária (identificar crianças, adultos e idosos). E quanto às ativações não binárias? Sim, isso também! Ele vai dar uma ativação analógica, ao contrário da função de passo. Vale lembrar que ele tem um gradiente suave também.

A fórmula é bem mais simples do que parece. Deixe-me explicar o que são as variáveis da fórmula:

• 1: é só um 1 mesmo.
• e: contante de Euler. É igual ao número de PI, só que de Euler. A constante é 2,718 281 828 459….
• x: a derivada da saída do seu neurônio. Ou seja, você pega a saída do seu neurônio (não é a saída da função de ativação, é a saída lá da função de primeiro grau), e deriva esse valor.

Se você não souber derivadas, não tem problema, há muitas bibliotecas que derivam coisas por aí. Mas se você puder correr atrás de saber mais sobre o tema, vai facilitar algumas coisas pra você quando nos aprofundarmos mais em redes neurais.

E só pra lembrar, essa função de ativação, diferentemente da função linear (step function), a saída sempre estará no intervalo de 0 e 1 em comparação com (-infinito, +infinito) da função linear, então temos nossas ativações limitadas em um intervalo.

Agora, se aplicarmos nossas imagens em três neurônios diferentes, e cada um usar a função Sigmoid como função de ativação, uma imagem classificada como “criança” terá a saída: criança=0.9,adulto=0.3, idoso=0.1.

Se sair adulto, teremos: criança=0.2,adulto=0.8,idoso=0.6, e se tivermos idoso: criança=0.2,adulto=0.6, idoso=0.8 (0,0,1).

Ótimo, temos nosso problema resolvido! Depois, é só colocar uns ifs (não façam isso, crianças) que está tudo certo. Existem outras funções de ativação, porém, não há necessidade de abordá-las aqui nesse momento – veremos mais quando estivermos falando de redes neurais em si.

Conclusão

Agora você já sabe o que é um neurônio e o que são funções de ativação – já é metade do conteúdo de uma rede neural (simples).

No próximo artigo vamos falar sobre como descobrimos os valores dos pesos e do bias. Depois disso, é show me the code!

Alguma dúvida? Deixe nos comentários!