Redes Neurais. Como encontrar os pesos corretos?

No artigo anterior, também sobre redes neurais, falamos sobre como é feita a classificação usando apenas um neurônio. Resumindo, você recebe alguns inputs do que você quer classificar (como uma imagem, por exemplo), multiplica isso com alguns pesos e, então, soma com o bias. Porém, como é que nós vamos saber os valores desses pesos todos? E do bias?

Provavelmente, você ainda não conseguiu abstrair a função dele na sua cabeça. Mas, tudo bem. Não se preocupe com isso (mas ele é importante viu, apesar de um neurônio funcionar sem ele).

Pois bem, vou te contar uma coisa. Nós (humanos) não vamos definir os valores desses caras. Mas, sim, algum algoritmo. Existem vários algoritmos que “descobrem” o valor dos pesos e dos bias.

Mas antes de falar sobre esses algoritmos, só pra construir uma linha de raciocínio simples, vamos pensar em um algoritmo de brute force. Ele é um pouquinho semelhante às técnicas existentes hoje em dia.

Treinamento

Muitas pessoas se perguntam como uma rede neural “aprende”. Explicando de uma forma simplificada (pois agora não é o momento para entender sobre esse assunto de forma aprofundada) e voltada apenas para um neurônio, o aprendizado se dá através da combinação dos pesos com o bias. Para você descobrir os valores certos dos pesos e do bias, você fará VÁRIAS classificações com VÁRIAS combinações de pesos e bias.

Cada vez que o seu neurônio roda, é feita uma classificação, seja ela correta ou errada. Pois bem, você pega essa classificação e verifica se o neurônio acertou ou errou. Conforme as ‘N’ classificações que vão se seguindo com seus diferentes valores dos pesos e bias, uma hora você vai chegar nos valores corretos.

Assim, você saberá quais são os pesos corretos que você precisa usar na hora de classificar uma imagem com uma criança, um adulto ou um idoso. Lembre-se, por ter 3 neurônios, você precisa fazer esse brute force para cada neurônio.

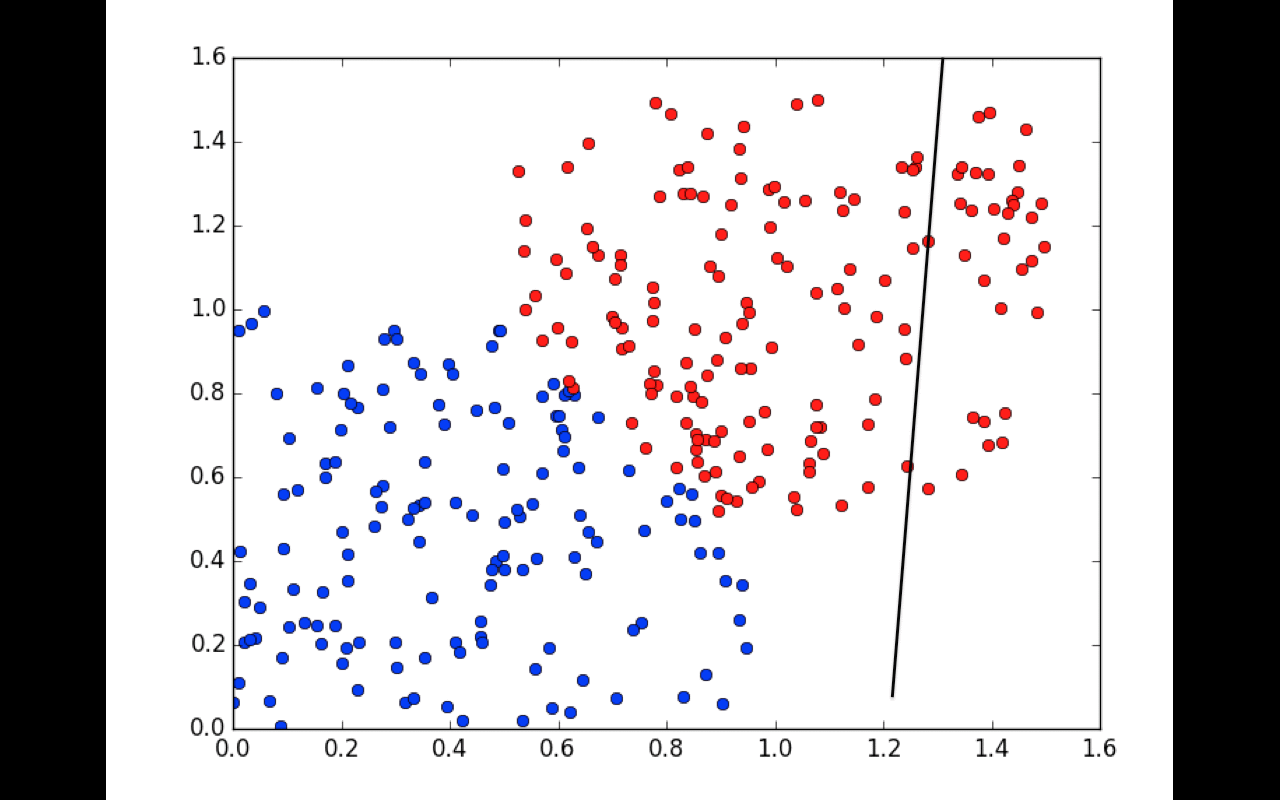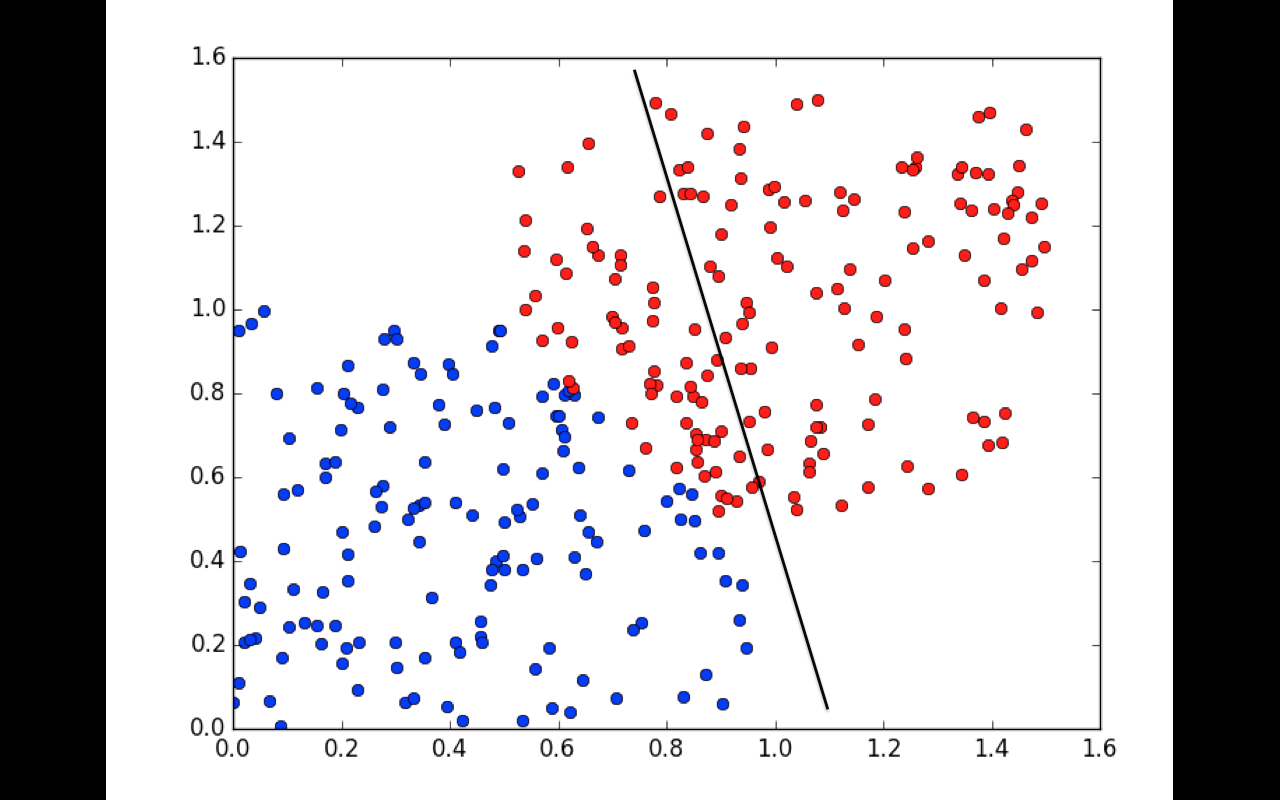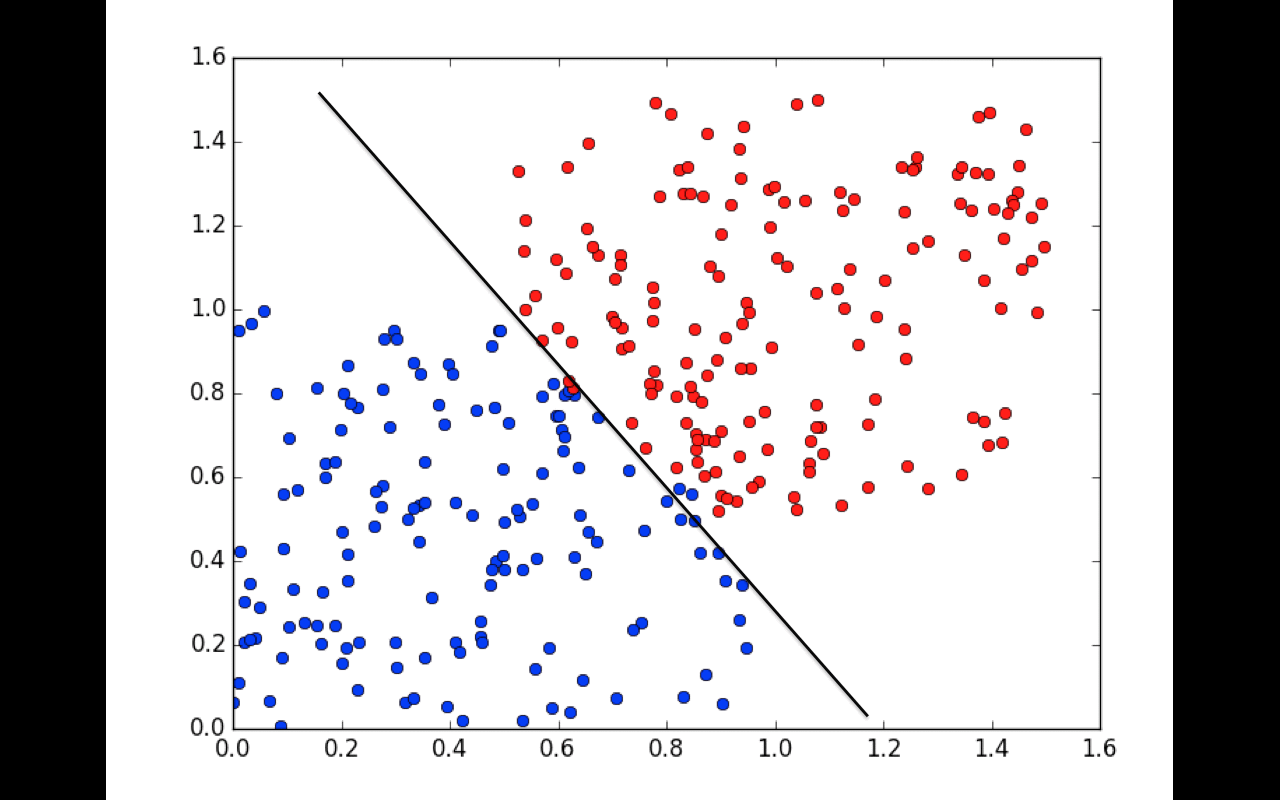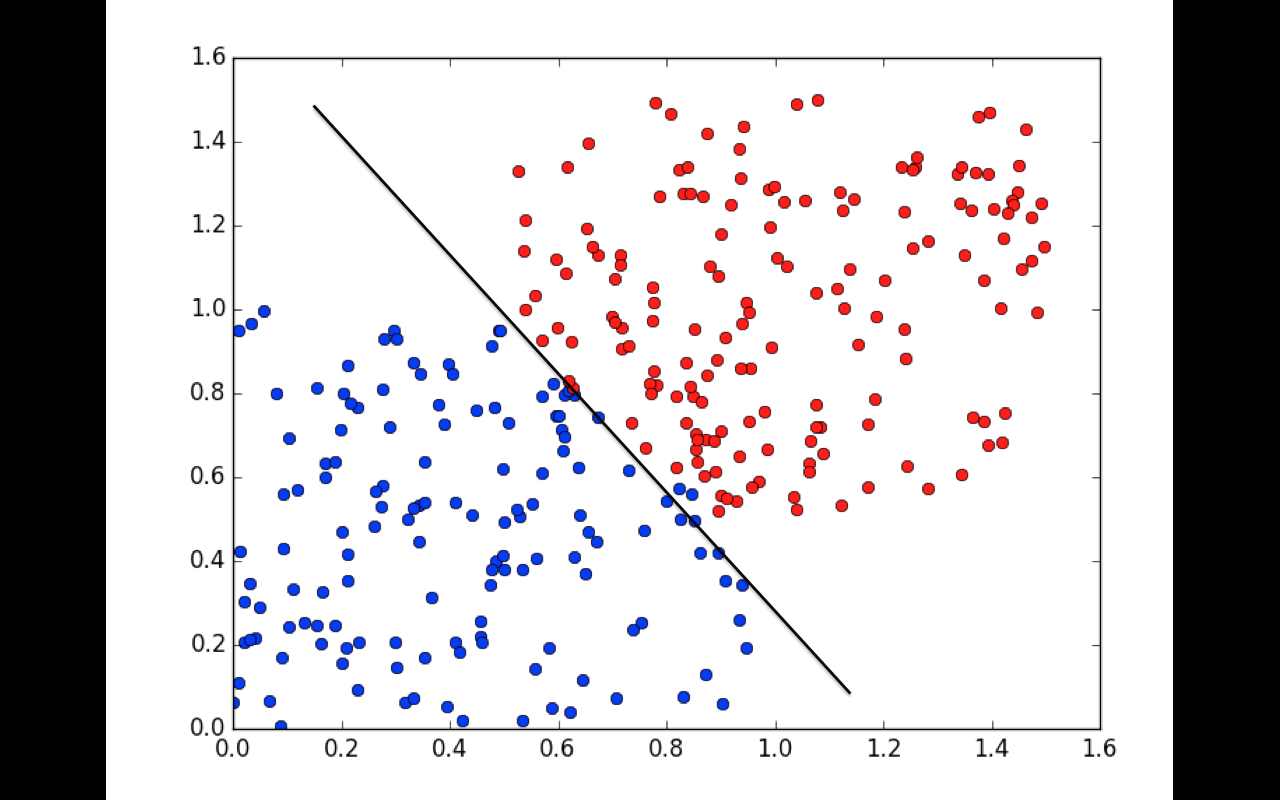
Nós chamamos isso de treinamento. É você tentar predizer/classificar dados que já sabe o resultado só para, depois, verificar se a saída do seu neurônio/rede neural, de fato, classificou tudo certinho. Introduzido a linha de raciocínio de um brute force, então, podemos seguir para algumas técnicas um pouco mais inteligentes, mas que ainda têm certa similaridade com o brute force.

Ajustando os pesos de forma inteligente

Todos sabem que o método de brute force, apesar de “funcionar”, não é performático e eficaz. Nesse caso, vamos usar uma outra técnica um pouco mais inteligente. Vamos continuar seguindo uma linha de raciocínio do brute force. Porém, não vamos atualizar nossos pesos de uma forma aleatória. Dessa vez, faremos um cálculo para saber o quanto temos de modificar em nossos pesos.

Até então, nosso processo foi sempre contínuo. Pegamos os inputs → multiplicamos com os pesos (sejam quais forem) →somamos o bias → usamos uma função de ativação, na saída dessas coisas todas, feitas nos passos anteriores, e, então, validamos a saída da função de ativação com um if ou uma outra implementação melhor.

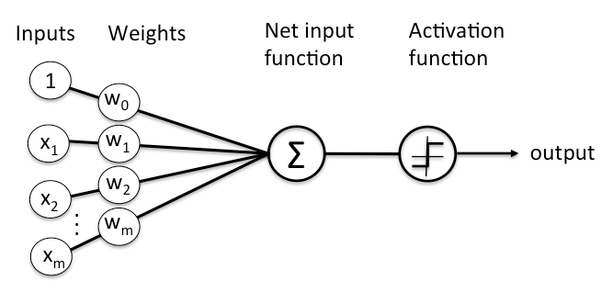
E todo esse processo nós seguimos com essa lógica para “frente”, sempre seguindo o próximo passo. Mas, em nenhum momento, nós voltamos no meio do algoritmo para corrigir algo. E é justamente isso que vamos fazer.

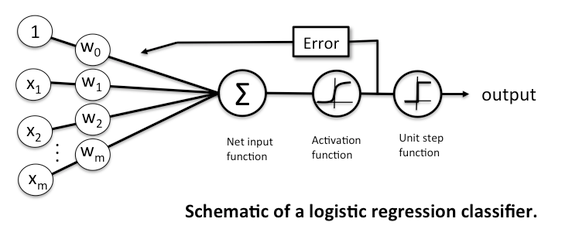
No final do processamento do seu neurônio você irá verificar se a sua saída está correta. Se ela estiver errada, nós vamos verificar o quão erradamente ela está usando o que chamamos de função de custo ou cost function (que já já falo mais dela).

Depois de ter essa informação, nós vamos rodar o nosso neurônio de novo e com novas combinações. Porém, como já falamos agora a pouco, dessa vez não vamos mudar os valores dos pesos e do bias de forma aleatória. Vamos verificar o quão errado foi a classificação do neurônio com nossa função de custo. E vamos ajustar os nossos pesos, de acordo com a saída desse cálculo.

Função de custo

Como a regressão é um cálculo usado para que seja possível fazer estimativas/predição/classificação, pode ser que, dependendo dos parâmetros que usarmos, façamos predições incorretas. Mas, como estamos trabalhando com uma base histórica de dados, onde temos nossos exemplos e suas saídas, podemos rodar nosso classificador em cima dessa base já classificada.

Assim, podemos testar os nossos parâmetros (nossos pesos) para nos certificarmos que as predições estão corretas (quando digo predição, estou dizendo de classificação também). E, nesse ato de rodar/“prever” fatos já ocorridos, podemos saber quais classificações estão erradas. Assim, como já comentamos no artigo a cima, podemos também saber o quão errado estão nossas saídas, usando função de custo. Essa função vai nos ajudar a minimizar esses erros. Exemplo disso é um valor aproximado de quanto nós temos de mexer, nos nossos parâmetros, para que possamos ajustar nossos pesos.

Existem várias funções de custo que você pode usar. A que vamos usar no nosso exemplo é o método dos mínimos quadrados médios. A fórmula para tal é esta que se apresenta na imagem abaixo. Mas não se assuste, vou explicar tudo:

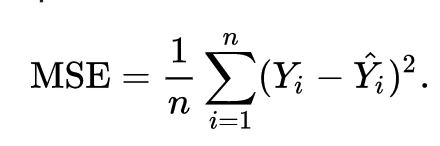
Parece assuntador né? Mas não é. É que matemático gosta de complicar as coisas. Pois bem, vamos lá. O que significa cada simbolo?

Basicamente a fórmula por escrito seria:

MSE = média da ((classificação correta — valor que foi classificado pelo nosso neuronio)²)

Ou seja, vamos pegar o valor do nosso neurônio e vamos subtrair pelo valor que era para ser predito. Exemplo: imagine que estamos testando nosso neurônio em uma casa que, durante 2 anos, se valorizou 100%. Porém, nosso neurônio previu que depois de dois anos, essa mesma casa se valorizou 180%.

Então, no fim vamos fazer o seguinte: média de ((200–180)²). Como estamos trabalhando com apenas um neurônio, a média não vai fazer muito sentido, mas vamos rever esse tópico. Pois bem, isso nos retornaria o valor ao qual teríamos de arrumar nos nossos pesos

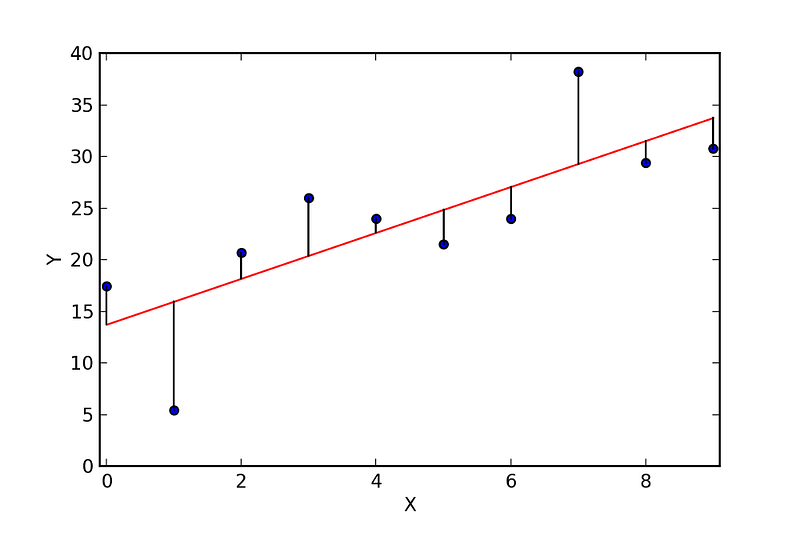
Para deixar um pouco mais ilustrado, vamos usar essa imagem acima. A “linha vermelha” é a nossa linha de regressão linear ou o nosso valor previsto (y^). E os pontos “azuis” são os nossos dados. A média do quadrado da distância dos pontos azuis (nossos dados) até a linha vermelha (valor previsto) deve ser o mínimo possível para obter a linha de regressão de melhor ajuste. A função de custo nos retorna o valor que vamos usar para traçar a linha preta, que liga os pontos azuis com a linha vermelha. Para traçar essa linha, vamos precisar usar um cara chamado gradiente descendente.

Gradiente descendente

O Gradiente Descente basicamente faz o que estamos fazendo manualmente — muda os valores dos pesos (ou parâmetros), pouco a pouco, até que tenhamos um mínimo (um valor que a predição esteja muito perto da saída correta).

Vamos utilizar um exemplo de uma regressão linear bastante simples (y^=b+x.w) e nós queremos achar os valores b e w que minimizam o erro de y^ (que é a classificação do nosso neurônio). Esse erro é o valor que nós achamos usando o algoritmo acima, o MSE.

Para saber mais sobre o gradiente descendente, olhe esse vídeo aqui onde ele explica de uma forma mais aprofundada.

A fórmula para o gradiente descendente é essa aqui:

A atualização dos pesos se segue por:

Peso n+1

isso significa que você está iterando sobre vários pesos. E o peso n+1 significa o próximo peso, ou se você quiser, pode pensar que é o peso atual, não tem problema;

Peso n

peso atual;

Momento

Responsável por escapar de mínimos locais. E o que são mínimos locais? Só para dar um brief, mínimos locais são valores aos quais seu algoritmo ficará tendencioso a usá-los. Então, pode ser que seu algoritmo sempre fique atualizando os pesos com os mesmos valores e esses valores nem sempre são os corretos.

Se você colocar um valor muito alto aqui (exemplo: 2.0 ou 3.0), seu algoritmo irá aprender mais rápido, porém não será tão eficaz. Caso coloque um valor muito baixo (0.00…01), seu algoritmo irá demorar mais para convergir (achar os pesos corretos). Porém, ele irá encontrar pesos melhores do que quando se usa um learning rate muito alto. Mais abaixo teremos uma sessão só para falar do learning rate e detalharei isso melhor.

Entrada

valor do resultado do neurônio (sum(x.w+b))

Delta

Derivada do valor da função de ativação (Sigmoid). Caso você não saiba sobre derivadas, pode olhar os conteúdos da khan academy sobre o tema.

Taxa de aprendizado

A taxa de aprendizado, ou learning rate, define o quão rápido nosso algorítimo irá aprender. Ele segue o mesmo principio do momento. Se você colocar um valor muito alto aqui (exemplo: 2.0 ou 3.0), seu algoritmo irá aprender mais rápido, porém não será tão eficaz. Caso coloque um valor muito baixo (0.00…01), seu algoritmo irá demorar mais para convergir (achar os pesos corretos). Porém, ele irá encontrar pesos melhores do que quando se usa um learning rate muito alto. Mais abaixo teremos uma sessão só para falar do learning rate.

Momento/Momentum

O Momentum é um assunto um tanto complexo. Mas ele, basicamente, é responsável por fazer com que sua atualização de peso não tome uma atualização muito brusca. Como por exemplo, seu peso atual é de 10.55 e você atualiza ele para 50.10. O momentum faz com que você continue seguindo a linha de valores próximos à 10.55, como 11 ou 9, por exemplo.

Taxa de aprendizado

A taxa de aprendizado é um hyper-parâmetro que controla o quanto estamos ajustando os pesos de nossa rede com relação ao gradiente descendente. Quanto menor o valor, mais devagar viajamos ao longo do declive descendente. Embora isso possa ser uma boa ideia (usando uma baixa taxa de aprendizado), em termos de garantir que não perderemos nenhum mínimo local, também pode significar que levaremos muito tempo para convergir.

Temos aqui uma baixa taxa de aprendizado:

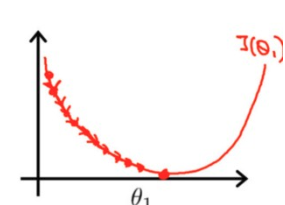
Perceba que, de pouquinho em pouquinho, nós conseguimos chegar ao mínimos de erro no nosso neurônio (usando a fórmula do MSE pra ver essa informação).

E qui temos um aprendizado usando uma taxa de aprendizado alta:

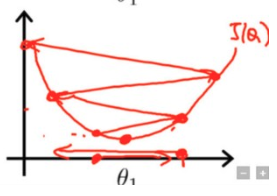
Perceba que nesse caso ele necessita de menos iterações para chegar ao nosso valor minimo de erro (mas tome cuidado com isso, valores altos para o learning rate não são recomendados).