A modelagem de tempo-para-evento é essencial para entender melhor as várias dimensões da experiência do usuário.

Ao aproveitar dados de tempo-para-evento censurados (dados que envolvem intervalos de tempo em que alguns desses intervalos podem se estender para além da análise de dados), as empresas podem obter insights sobre pontos de dor no ciclo de vida do consumidor para aprimorar a experiência geral do usuário.

Apesar de sua prevalência, os dados de tempo-para-evento censurados são frequentemente negligenciados, levando a previsões dramaticamente tendenciosas.

Na Uber, estamos interessados em investigar o tempo que leva para um passageiro fazer uma segunda viagem após a primeira viagem na plataforma. Muitos de nossos passageiros se envolvem com a Uber pela primeira vez por meio de referências ou promoções.

Sua segunda corrida é um indicador crítico de que os passageiros estão encontrando valor no uso da plataforma e estão dispostos a se envolver conosco em longo prazo.

No entanto, modelar o tempo para a segunda corrida é complicado. Por exemplo, alguns passageiros simplesmente não fazem corridas com frequência.

Quando analisamos esses dados de tempo-para-evento antes da segunda corrida desse passageiro, consideramos seus dados censurados.

Situações semelhantes existem em outras empresas e em todos os setores. Por exemplo, suponha que um site de e-commerce esteja interessado no padrão de compra recorrente dos clientes.

No entanto, devido ao padrão diversificado de comportamento do cliente, a empresa pode não ser capaz de observar todas as compras recorrentes para todos os clientes, resultando em dados censurados.

Em outro exemplo, suponha que uma empresa de publicidade esteja interessada no comportamento recorrente de cliques em anúncios de seus usuários.

Devido aos interesses distintos de cada usuário, a empresa pode não conseguir observar todos os cliques feitos por seus clientes.

Os usuários podem não ter clicado nos anúncios até o final do estudo. Isso resultará em tempo censurado para os dados do próximo clique.

Na modelagem de dados de tempo-para-evento censurados, para cada indivíduo de interesse indexado por , podemos observar dados no seguinte formato:

• (Ti, Li)

Aqui, Li é o rótulo de censura; Li = 1 se o evento de interesse for observado; e Li = 0 se o evento de interesse for censurado. Quando Li – 1, Ti denota o tempo-para-o-evento de interesse. Quando Li = 0, Ti , denota o período de tempo até que a censura aconteça.

Vamos continuar com o exemplo do tempo para a segunda corrida na Uber: se um passageiro fizer uma segunda corrida 12 dias após a primeira, essa observação será registrada como (12, 1).

Em outro caso, um passageiro fez a primeira corrida, 60 dias se passaram, e eles ainda não retornaram ao aplicativo para dar uma segunda volta em determinada data limite. Essa observação é registrada como (60,0). A situação é ilustrada na figura abaixo:

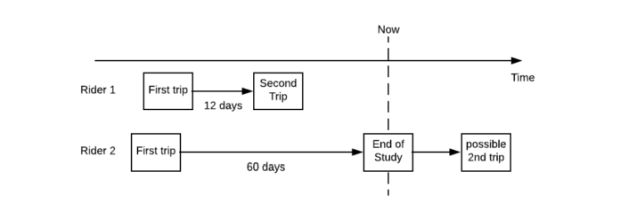
Existe um oceano de literatura de análise de sobrevivência e mais de um século de pesquisa estatística já foi feita nessa área; e muito disso pode ser simplificado usando o framework de programação probabilística. Neste artigo, vamos ver como usar a linguagem de programação probabilística Pyro para modelar dados censurados de tempo-para-evento.

Relação com modelagem de churn

Antes de prosseguir, vale a pena mencionar que muitos profissionais da indústria contornam esse desafio de dados censurados de tempo-para-evento estabelecendo rótulos definidos artificialmente como “churn”.

Por exemplo, uma empresa de comércio eletrônico pode definir um cliente como “churned” se ele ainda não retornou ao site para fazer outra compra nos últimos 40 dias.

A modelagem de churn permite que os profissionais massageiem as observações em um padrão clássico de classificação binária.

Como resultado, a modelagem de churn se torna muito direta com ferramentas prontas como o scikit-learn e o XGBoost. Por exemplo, os dois passageiros acima seriam rotulados como “not churned” e “churned”, respectivamente.

Embora a modelagem de churn funcione em certas situações, ela não funciona necessariamente para a Uber. Por exemplo, alguns passageiros podem usar a Uber apenas quando estão em uma viagem de negócios.

Se esse passageiro hipotético fizer uma viagem de trabalho a cada seis meses, poderemos acabar classificando erradamente esse passageiro como churned. Como resultado, a conclusão que tiramos de um modelo de churn pode ser enganosa.

Também estamos interessados em fazer interpretações a partir desses modelos para elucidar a contribuição de diferentes fatores para o comportamento do usuário observado.

Como resultado, o modelo não deve ser uma caixa preta. Adoraríamos ter a capacidade de abrir o modelo e tomar decisões de negócios mais informadas com ele.

Para conseguir isso, podemos alavancar o Pyro, uma ferramenta flexível e expressiva open source para programação probabilística.

Pyro para modelagem estatística

Criado na Uber, o Pyro é uma linguagem de programação probabilística universal escrita em Python, construída na biblioteca PyTorch para cálculos de tensores.

Se você vem de um background de estatísticas com conhecimento mínimo de modelagem Bayesiana ou se você estiver mexendo com ferramentas de deep learning como TensorFlow ou PyTorch, você está com sorte.

A tabela a seguir resume alguns dos projetos mais populares para programação probabilística:

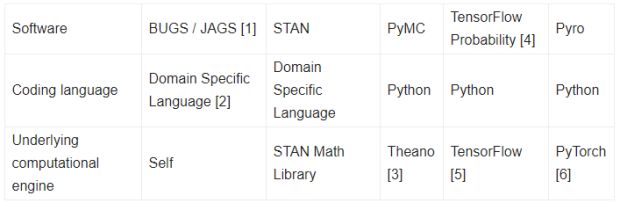
Abaixo, destacamos algumas características importantes sobre esses diferentes projetos de software:

• 1. BUGS/JAGS são os primeiros exemplos do que veio a ser conhecido como programação probabilística. Eles estão em desenvolvimento ativo e uso há mais de duas décadas no campo estatístico.
• 2. No entanto, BUGS/JAGS são projetados e desenvolvidos principalmente a partir do zero. Como resultado, a especificação do modelo é feita usando a linguagem específica do domínio. Além disso, programadores probabilísticos invocam BUGS/JAGS a partir de wrappers em R e MATLAB. Os usuários precisam alternar entre linguagens e arquivos de codificação, o que é um pouco inconveniente.
• 3. O PyMC depende de um backend Theano. No entanto, o projeto Theano foi recentemente descontinuado.
• 4. A Probabilidade do TensorFlow (TFP) começou originalmente como um projeto chamado Edward. O projeto de Edward foi lançado no projeto TFP.
• 5. TFP usa o TensorFlow como seu mecanismo de computação. Como resultado, ele suporta apenas gráficos computacionais estáticos.
• 6. O Pyro usa o PyTorch como mecanismo de computação. Como resultado, ele suporta gráficos computacionais dinâmicos. Isso permite que os usuários especifiquem modelos que são diversos em termos de fluxo de dados e são muito flexíveis.

Em suma, o Pyro está posicionado na interseção muito benéfica das mais poderosas cadeias de ferramentas de deep learning (PyTorch), ao mesmo tempo em que se apoia nos ombros de décadas de pesquisa estatística. O resultado é uma linguagem de modelagem probabilística imensamente concisa e poderosa, mas flexível.

Modelando dados de btempo-para-evento censurados

Agora, vamos pular para a forma como modelamos dados censurados de tempo-para-evento. Graças ao Google Colab, os usuários podem conferir exemplos extensivos do código e iniciar a modelagem de dados sem instalar o Pyro e o PyTorch. Você pode até mesmo duplicar e brincar com a pasta de trabalho.

Definição de modelo

Para o propósito deste artigo, definimos os dados de tempo-para-evento como (Ti, Li), com Ti como o tempo-para-evento e Li como o rótulo de censura binária. Nós definimos o real tempo-para-evento como Tºi, o que pode não ser observado.

Definimos o tempo de censura como C, que, por simplicidade, assumimos que é um número fixo conhecido. Em resumo, podemos modelar esse relacionamento como:

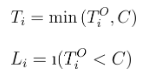
Assumimos Tºi que segue a distribuição exponencial com parâmetro de escala λi, uma variável dependente da seguinte relação linear com o indicador de interesse Xi:

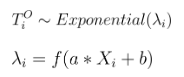
Aqui, f é uma função do softplus, garantindo assim que λi permanece positivo. Finalmente, assumimos que α e b seguem a distribuição normal como sua distribuição anterior. Para o propósito deste artigo, estamos interessados em avaliar a distribuição posterior de α e b.

Gerando dados artificiais

Primeiro, importamos todos os pacotes necessários em Python:

import pyro 
import torch 
import seaborn as sns 
import pyro.distributions as dist 
from pyro import infer, optim
from pyro.infer.mcmc import HMC, MCMC
from pyro.infer import EmpiricalMarginal

assert pyro.__version__.startswith('0.3')

Para gerar dados experimentais, executamos as seguintes linhas:

n = 500
a = 2
b = 4
c = 8

x = dist.Normal(0, 0.34).sample((n,)) # Note [1]
  
link = torch.nn.functional.softplus(torch.tensor(a*x + b))
# note below, param is rate, not mean
y = dist.Exponential(rate=1 / link).sample()  

truncation_label = (y > c).float()

y_obs = y.clamp(max=c)

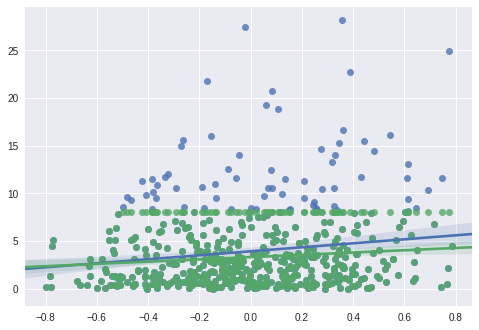
sns.regplot(x.numpy(), y.numpy())
sns.regplot(x.numpy(), y_obs.numpy()) ## Note [2] 

Parabéns! Você acabou de executar sua primeira função Pyro na linha com Note [1]. Aqui nós desenhamos amostras de uma distribuição normal. Usuários cuidadosos podem ter notado que essa operação intuitiva é muito semelhante ao nosso fluxo de trabalho no Numpy.

No final do bloco de código acima (Note 2), geramos um gráfico de regressão de Ti (verde), Tºi (azul) contra Xi, respectivamente. Se não considerarmos a censura de dados, subestimamos a inclinação do modelo.

Construindo modelos

Com esses dados novos, mas censurados, podemos começar a construir modelos mais precisos. Vamos começar com a função de modelo abaixo:

def model(x, y, truncation_label): ## Note [1] 
  a_model = pyro.sample("a_model", dist.Normal(0, 10)) ## Note [2] 
  b_model = pyro.sample("b_model", dist.Normal(0, 10))
  
  link = torch.nn.functional.softplus(a_model * x + b_model) ## Note [3] 
  
  for i in range(len(x)):
    y_hidden_dist = dist.Exponential(1 / link[i]) ## Note [4] 
    
    if truncation_label[i] == 0: 
      ## Note [5] 
      y_real = pyro.sample("obs_{}".format(i), 
                           y_hidden_dist,
                           obs = y[i])
    else:
      ## Note [6]
      truncation_prob = 1 - y_hidden_dist.cdf(y[i])
      pyro.sample("truncation_label_{}".format(i), 
                  dist.Bernoulli(truncation_prob), 
                  obs = truncation_label[i])

No trecho de código acima, destacamos as seguintes notas para esclarecer melhor nosso exemplo:

• Nota 1: No geral, uma função de modelo é um processo de descrever como os dados são gerados. Esse exemplo de função de modelo informa como geramos y ou truncation_label a partir do vetor de entrada x.
• Nota 2: Nós especificamos uma distribuição prévia de α e b aqui e fazemos uma amostra deles usando a função pyro.sample. O Pyro tem uma enorme família de distribuições aleatórias no projeto PyTorch, assim como no próprio projeto Pyro.
• Nota 3: Conectamos as entradas x, α, e b no vetor λ denotado por link variável aqui.
• Nota 4: Especificamos a distribuição real do tempo-para-evento Tºi usando a distribuição exponencial com link de vetor de parâmetro de escala.
• Nota 5: Para observação i , se observarmos os dados de tempo-para-evento, então o contrastamos com a observação verdadeira y [i].
• Nota 6: Se os dados forem censurados para observação i, o rótulo de truncagem (igual a 1 aqui) segue a distribuição de Bernoulli. A probabilidade de ver dados truncados é a CDF de Tºi em um ponto Ti. Nós fizemos uma amostra a partir da distribuição de Bernoulli e contrastamos com a observação real de truncation_label [i].

Para mais informações sobre modelagem Bayesiana e usando o Pyro, confira nosso tutorial introdutório.

Calculando a inferência usando Hamiltonian Monte Carlo

O Hamiltoniano Monte Carlo (HMC) é uma técnica popular quando se trata de calcular a inferência Bayesiana.

Estimamos e usando o HMC, abaixo:

pyro.clear_param_store()

# note [1] 
hmc_kernel = HMC(model,
                 step_size = 0.1, 
                 num_steps = 4)


# Note [2] 
mcmc_run = MCMC(hmc_kernel, 
                num_samples=5,
                warmup_steps=1).run(x, y, truncation_label)


# Note [3] 
marginal_a = EmpiricalMarginal(mcmc_run, 
                               sites="a_model")


# Note [4] 
posterior_a = [marginal_a.sample() for i in range(50)] 

sns.distplot(posterior_a)

O processo acima pode levar muito tempo para ser executado. A lentidão vem em grande parte devido ao fato de que estamos avaliando o modelo através de cada observação sequencialmente.

Para acelerar o modelo, podemos vetorizar usando pyro.plate e pyro.mask, conforme demonstrado abaixo:

def model(x, y, truncation_label):
  a_model = pyro.sample("a_model", dist.Normal(0, 10)) 
  b_model = pyro.sample("b_model", dist.Normal(0, 10))
  
  link = torch.nn.functional.softplus(a_model * x + b_model) 
  
  with pyro.plate("data"):
    y_hidden_dist = dist.Exponential(1 / link) 
    
    with pyro.poutine.mask(mask = (truncation_label == 0)): 
      pyro.sample("obs", y_hidden_dist,
                  obs = y)
      
    with pyro.poutine.mask(mask = (truncation_label == 1)):
      truncation_prob = 1 - y_hidden_dist.cdf(y)
      pyro.sample("truncation_label", 
                  dist.Bernoulli(truncation_prob), 
                  obs = torch.tensor(1.))

No trecho de código acima, começamos especificando o kernel do HMC usando o modelo especificado. Em seguida, executamos o MCMC contra x, y e o truncation_label.

O objeto de resultado amostrado MCMC é convertido em um objeto EmpiricalMarginal que nos ajuda a fazer a inferência ao longo do parâmetro a_model.

Por fim, extraímos amostras da distribuição posterior e criamos um gráfico com nossos dados, mostrado abaixo:

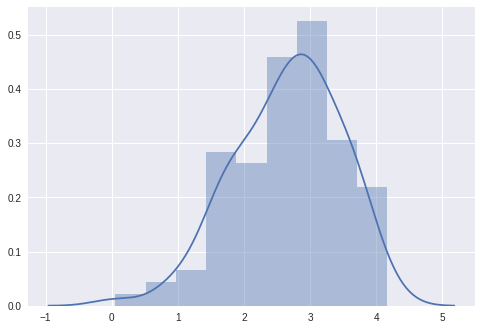
Podemos ver que as amostras estão agrupadas em torno do valor real de 2.0.

Acelerando a estimativa usando a inferência variacional

A inferência variacional estocástica (SVI) é uma ótima maneira de acelerar a inferência Bayesiana com grandes quantidades de dados. Por enquanto, é suficiente prosseguir com o conhecimento de que uma função guia é uma aproximação da distribuição posterior desejada.

A especificação de uma função guia pode acelerar drasticamente a estimativa de parâmetros. Para permitir a inferência variacional estocástica, definimos uma função guia como:

guide = AutoMultivariateNormal(model)

Usando uma função guia, podemos aproximar as distribuições posteriores de parâmetros e como distribuições normais, onde seus parâmetros de localização e escala são especificados por parâmetros internos, respectivamente.

Treinando o modelo e inferindo resultados

O processo de treinamento de modelo com o Pyro é semelhante à otimização iterativa padrão em deep learning. Abaixo, especificamos o treinador SVI e iteramos através de etapas de otimização:

pyro.clear_param_store()
  
adam_params = {"lr": 0.01, "betas": (0.90, 0.999)}
optimizer = optim.Adam(adam_params)

svi = infer.SVI(model, 
                guide, 
                optimizer, 
                loss=infer.Trace_ELBO())

losses = []
for i in range(5000):
  loss = svi.step(x, y_obs, truncation_label)
  losses.append(loss)

  if i % 1000 == 0:
    print(', '.join(['{} = {}'.format(*kv)
                     for kv in guide.median().items()]))

print('final result:')
for kv in sorted(guide.median().items()):
  print('median {} = {}'.format(*kv))

Se tudo correr conforme o planejado, podemos ver a impressão da execução acima. Neste exemplo, recebemos os seguintes resultados, cujas médias são muito próximas do valor real de e especificado:

a_model = 0.009999999776482582, b_model = 0.009999999776482582
a_model = 0.8184720873832703, b_model = 2.8127853870391846
a_model = 1.3366154432296753, b_model = 3.5597035884857178
a_model = 1.7028049230575562, b_model = 3.860581874847412
a_model = 1.9031578302383423, b_model = 3.9552347660064697
final result:
median a_model = 1.9155923128128052
median b_model = 3.9299516677856445

Também podemos verificar se o modelo convergiu através do código abaixo e chegar à Figura 3:

sns.plt.plot(losses)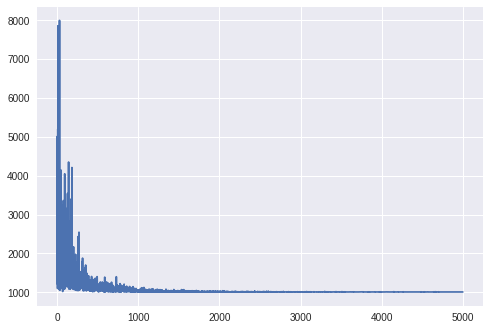

Podemos plotar a distribuição posterior aproximada usando a função guide.quantiles():

N = 1000
for name, quantiles in guide.quantiles(torch.arange(0., N) / N).items():
  quantiles = np.array(quantiles)
  pdf = 1 / (quantiles[1:] - quantiles[:-1]) / N
  x = (quantiles[1:] + quantiles[:-1]) / 2
  sns.plt.plot(x, pdf, label=name)
  
sns.plt.legend()
sns.plt.ylabel('density')

Podemos ver que as funções guia se centram no valor real de e b, respectivamente abaixo:

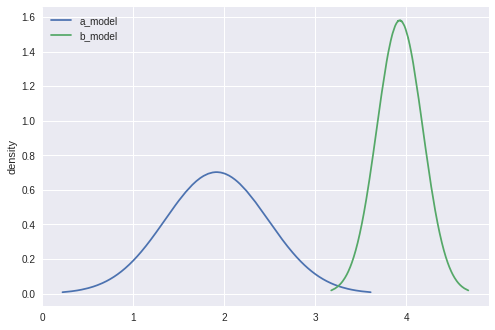
Próximos passos

Esperamos que você aproveite o Pyro para sua própria modelagem de dados censurados de tempo-para-evento.

Para começar a usar o software open source, confira o site oficial do Pyro para obter exemplos adicionais, incluindo um tutorial introdutório e um repositório de sandbox.

Em artigos futuros, pretendemos discutir como você pode alavancar recursos adicionais do Pyro para acelerar a computação do SVI, incluindo o uso da API da placa para o processo em lote em amostras de formato similar.

Interessado em trabalhar no Pyro e outros projetos da Uber AI? Considere candidatar-se a um cargo na nossa equipe!

***

Este artigo é do Uber Engineering. Ele foi escrito por Hesen Peng e Fritz Obermeyer. A tradução foi feita pela Redação iMasters com autorização. Você pode conferir o original em: https://eng.uber.com/modeling-censored-time-to-event-data-using-pyro/