Olá, pessoal!

Muitos programadores se assustam um pouco quando falamos de recursividade, mas é quase certo que você já conhece o conceito e/ou já precisou dele.

Também já deve ter escutado sobre funções recursivas serem mais lentas que loops tradicionais, mas será que é isso mesmo?

Recursividade é uma técnica bastante popular para resolver problemas que possam ser decompostos em partes menores, problemas como a sequência fibonacci ou percorrer estruturas de dados, por exemplo.

No entanto, existem alguns problemas que cercam o uso de recursividade. Não é nenhum segredo que, de maneira geral, elas são mais lentas que um laço de repetição tradicional. Além disso, há um limite de chamadas de funções que podemos realizar, e é esse o ponto que tocaremos hoje.

Primeiro vamos entender isso melhor. Por que há um limite de chamadas?

A aplicação contém uma estrutura chamada pilha de chamadas. Essa estrutura de dados funciona como uma pilha comum, armazenando o local para onde a execução do programa deve retornar quando uma função é chamada.

Na prática funciona da seguinte maneira: sempre que você realiza uma chamada para qualquer função no seu código (mesmo as que não são recursivas), um ponteiro com o local de execução código é armazenado nesta pilha.

Depois disso, a função é executada. Ao terminar sua execução, o ponteiro é restaurado da pilha e o código volta para seu local de origem.

Vamos criar uma função que simplesmente escreve “Hello” no console:

let helloFunction() =
    printf "Hello"

[<EntryPoint>]
let main argv =  
    helloFunction()
    |> ignore

Como você pode ver na imagem abaixo, se colocarmos um breakpoint podemos visualizar a pilha de chamadas:

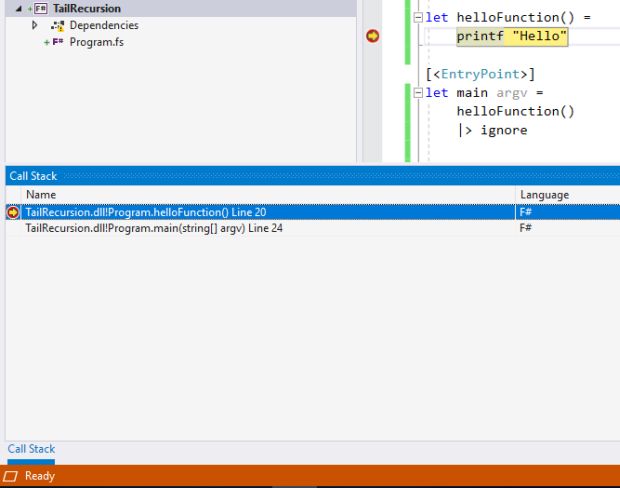
Apesar de super útil, a pilha de chamadas pode causar um erro bastante popular: o Stack Overflow. Você já deve ter escutado esse nome quando foi tirar uma dúvida na internet. Pois é, esse erro é tão famoso que o site fez uma brincadeira/homenagem a ele.

Esse erro acontece porque a pilha de chamadas possui um limite fixo de memória. Isso pode variar de linguagem para linguagem, mas geralmente não é muito diferente de 1MB. Então, se realizarmos mais chamadas do que o suportado, acabará a memória e essa exceção será lançada.

Fazer um exemplo simples: uma função recursiva que soma os números de uma lista. Vamos lá:

let rec sum list =
    match list with
    | [] -> 0
    | head::tail -> head + sum tail

Se a lista estiver vazia, eu simplesmente retorno zero. Caso contrário, retorno a soma do head (primeiro elemento da lista) com a soma do tail (restante da lista). Até aqui, tudo tranquilo.

Vamos criar uma lista de 1000 posições e chamar essa função:

[<EntryPoint>]
let main argv =  
    List.init 1000 (fun index -> index)
    |> sum
    |> Console.WriteLine

    Console.ReadKey()
    |> ignore

    0

Sucesso!

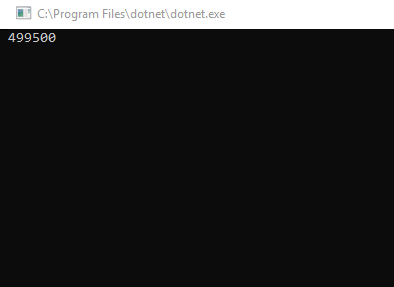
Mas e se aumentarmos o tamanho da lista para 10000?

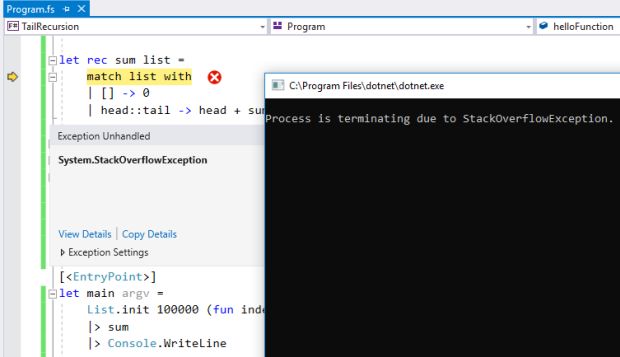
Ops, talvez não tenha sido tanto sucesso assim. Acabamos de estourar a pilha de chamadas.

Isso acontece porque não estamos utilizando recursão em cauda.

Mas afinal de contas, o que é isso?

Recursão em cauda é um tipo específico de recursividade que está bastante relacionada ao que chamamos de Tail Call. Uma tail call ocorre quando é feita uma chamada recursiva, garantindo que não há mais nada para ser executado depois da chamada da função recursiva.

Com isso, é justo falar que o retorno da função que realizou a chamada recursiva é o mesmo retorno da função chamada. Afinal, nada será executado depois disso.

Por conta disso, o programa não precisa manter armazenado o ponteiro com o endereço de retorno. Afinal, pode-se assumir que o local é o mesmo da nova chamada.

Internamente o compilador irá substituir a chamada recursiva (quando a tail recursion é utilizada) por uma instrução de JUMP, voltando para a primeira linha de código da função e melhorando, inclusive, a performance, por não precisarmos alocar nada na pilha de chamadas.

Agora precisamos entender o motivo do nosso código não estar realizando a tail call. Uma tail call só é utilizada quando a função recursiva é chamada em uma tail position.

E o jeito mais simples de definir a tail position, é: ela é última instrução que acontece. Só isso. É só um nome bonito para uma coisa muito simples.

Veja alguns exemplos:

let function1 n =
    n //Tail position

let function2 n =
    if n % 2 = 0
        then n //Tail position
        else 0 //Tail position

let function3 n =
    let value = n + 1
    value //Tail position

let function4 n =
    match n with
    | 2 -> n //Tail position
    | _ -> 0 //Tail position

Repare na function4. Parece que o nosso código estava em uma tail position afinal de contas, certo? Errado.

Ele quase estava, mas a expressão em nosso patern matching anterior era:

let rec sum list =
    match list with
    | [] -> 0 //Tail position
    | head::tail -> head + sum tail //Não é uma tail position

Apesar de parecer muito, a chamada da função ocorre antes da soma com o head, portanto, não estamos em uma tail position, e por consequência disso, não estamos realizando uma tail call.

Neste ponto, a solução já deve estar óbvia pra você – tudo que precisamos fazer é que a chamada da função esteja na tail position. Para fazer isso vamos fazer uma nova função.

Essa nova função será bastante semelhante à anterior, mas neste caso vamos utilizar um acumulador via parâmetro, ao invés de acumular os retornos – simples assim.

Para melhorar o consumo dessa função vamos manter o acumulador em uma chamada interna, sem a necessidade do consumidor informar qualquer valor.

let tailRecursionSum list =
    let rec _internalSum list acc =
        match list with
        | [] -> acc
        | head::tail -> _internalSum tail (head + acc)

    _internalSum list 0

Talvez o código pareça um pouco menos natural pra você, mas quando falamos de programação funcional, recursão em cauda é muito importante, visto que se dá preferência para recursividade ao invés de laços de repetição.

Agora vamos testar nosso novo código:

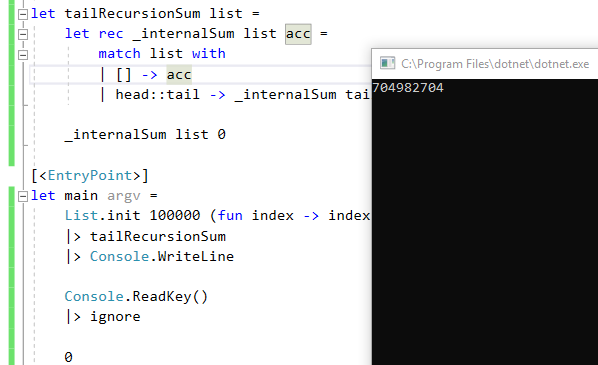
Sem StackOverflow!

De fato, se colocarmos um breakpoint no código e olharmos a pilha de chamada, ela nunca aumenta:

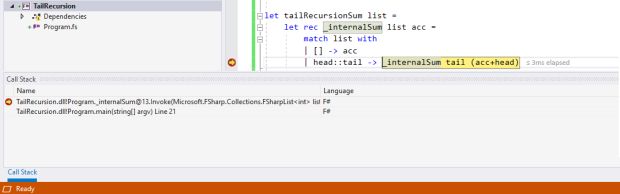
Legal, né?

Com isso você acaba de ver uma implementação de recursão em cauda, mas como podemos checar se tudo está de acordo?

O teste mais simples é a checagem da pilha de chamadas. Outro ponto é simplesmente executar o algoritmo com entradas maiores, mas claro: são testes do tipo “tentativa e erro”.

Se você quiser fazer uma análise mais profunda, pode utilizar o IL Disassembler para ver o código gerado.

Atenção

Se você não conhece o IL, sugiro que verifique este link. De maneira rápida (e incompleta), o IL é a linguagem intermediária gerada pelo .NET.

Quando compilamos nosso código em .NET ele é transformado nessa linguagem, que por sua vez é compilada em tempo de execução (JIT).

Para usar o IL Disassembler você precisa abrir o console de desenvolvedor do VS. Para isso, basta procurar por “developer command” no Windows que ele será listado.

Navegue até a pasta do seu projeto (utilize o comando cd normalmente) e depois disso execute o comando: ildasm nome-do-exe.exe, conforme na imagem abaixo:

Agora navegaremos pelo IL DASM. Primeiro daremos uma olhada na primeira função sum, que gerava o problema de StackOverflow:

.method public static int32  sum(class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> list) cil managed
{
  // Code size       39 (0x27)
  .maxstack  4
  .locals init (class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> V_0,
           class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> V_1,
           class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> V_2,
           int32 V_3)
  IL_0000:  ldarg.0
  IL_0001:  stloc.0
  IL_0002:  ldloc.0
  IL_0003:  call       instance class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<!0> class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>::get_TailOrNull()
  IL_0008:  brfalse.s  IL_000c
  IL_000a:  br.s       IL_000e
  IL_000c:  ldc.i4.0
  IL_000d:  ret
  IL_000e:  ldloc.0
  IL_000f:  stloc.1
  IL_0010:  ldloc.1
  IL_0011:  call       instance class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<!0> class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>::get_TailOrNull()
  IL_0016:  stloc.2
  IL_0017:  ldloc.1
  IL_0018:  call       instance !0 class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>::get_HeadOrDefault()
  IL_001d:  stloc.3
  IL_001e:  ldloc.3
  IL_001f:  ldloc.2
  IL_0020:  call       int32 Program::sum(class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>)
  IL_0025:  add
  IL_0026:  ret
} // end of method Program::sum

Talvez essa linguagem pareça bastante estranha para você, mas o ponto aqui não é entendermos todas as instruções – vamos focar na instrução call, ela acontece em quatro momentos distintos:

• 1. IL 003: call para a função get_TailOrNull();
• 2. IL 011: call para a função get_TailOrNull();
• 3. IL 018: call para a função get_HeadOrDefault();
• 4. IL 020: call para a função sum;

A linha 20 demonstra que a recursão está acontecendo, portanto, a pilha de chamadas acaba sendo preenchida normalmente.

Agora vamos ver a função tailRecursionSum:

.method public static int32  tailRecursionSum(class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> list) cil managed
{
  // Code size       17 (0x11)
  .maxstack  5
  .locals init (class [FSharp.Core]Microsoft.FSharp.Core.FSharpFunc`2<class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>,class [FSharp.Core]Microsoft.FSharp.Core.FSharpFunc`2<int32,int32>> V_0)
  IL_0000:  newobj     instance void Program/_internalSum@13::.ctor()
  IL_0005:  stloc.0
  IL_0006:  ldloc.0
  IL_0007:  ldarg.0
  IL_0008:  ldc.i4.0
  IL_0009:  tail.
  IL_000b:  call       !!0 class [FSharp.Core]Microsoft.FSharp.Core.FSharpFunc`2<class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>,int32>::InvokeFast<int32>(class [FSharp.Core]Microsoft.FSharp.Core.FSharpFunc`2<!0,class [FSharp.Core]Microsoft.FSharp.Core.FSharpFunc`2<!1,!!0>>, !0, !1)
  IL_0010:  ret
} // end of method Program::tailRecursionSum

A primeira grande diferença é o tamanho do código gerado. Essa função parece bem mais simples que a anterior, certo?

Além disso, também temos uma instrução call na última linha. O que isso significa?

Significa que estamos vendo a função errada. Precisamos abrir a função interna – esta, sim, possui o código real.

A função aninhada não é listada diretamente, mas podemos abri-la conforme a imagem a seguir:

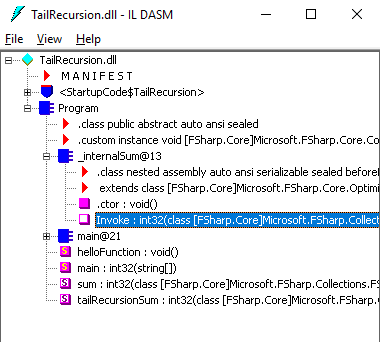
Agora daremos uma olhada no código:

.method public strict virtual instance int32 
        Invoke(class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> list,
               int32 acc) cil managed
{
  // Code size       40 (0x28)
  .maxstack  7
  .locals init (class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> V_0,
           class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> V_1,
           class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32> V_2,
           int32 V_3)
  IL_0000:  ldarg.1
  IL_0001:  stloc.0
  IL_0002:  ldloc.0
  IL_0003:  call       instance class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<!0> class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>::get_TailOrNull()
  IL_0008:  brfalse.s  IL_000c
  IL_000a:  br.s       IL_000e
  IL_000c:  ldarg.2
  IL_000d:  ret
  IL_000e:  ldloc.0
  IL_000f:  stloc.1
  IL_0010:  ldloc.1
  IL_0011:  call       instance class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<!0> class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>::get_TailOrNull()
  IL_0016:  stloc.2
  IL_0017:  ldloc.1
  IL_0018:  call       instance !0 class [FSharp.Core]Microsoft.FSharp.Collections.FSharpList`1<int32>::get_HeadOrDefault()
  IL_001d:  stloc.3
  IL_001e:  ldloc.2
  IL_001f:  ldarg.2
  IL_0020:  ldloc.3
  IL_0021:  add
  IL_0022:  starg.s    acc
  IL_0024:  starg.s    list
  IL_0026:  br.s       IL_0000
} // end of method _internalSum@13::Invoke

Se notarmos, ainda ocorrem três instruções de call, mas desta vez, apenas para obter o head e o tail da lista.

Ao invés de termos uma última call para a própria função, temos uma instrução br.s que funciona como um JUMP para a instrução listada como parâmetro. Ou seja, temos um JUMP para a primeira linha de código da função.

Esse JUMP está ocorrendo logo depois de duas instruções starg.s, que são utilizadas para armazenar um valor em um argumento, então, o que nosso código está de fato fazendo, é atualizando o valor dos parâmetros em cada iteração e utilizando um JUMP para voltar à primeira linha.

Por conta disso, nada de StackOverflows!

Como eu disse antes, o entendimento desse tipo de implementação é fundamental para escrevermos um código funcional de alta performance e evitar problemas bobos como o StackOverflow.

Muitas vezes não paramos para realizar uma autocrítica de como estamos desenvolvendo, mas esse é um ótimo exemplo de um código que pode funcionar “na sua máquina” e em produção começar a gerar exceções.

Espero que tenham gostado deste tipo de artigo!

Qualquer dúvida ou sugestão, deixem nos comentários!

Até mais!