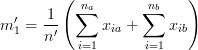No artigo anterior, começamos com exemplos de por que as propriedades monóide e grupo de distribuições Gaussianas são úteis na prática. Nesta segunda parte, vamos dar uma olhada em como é o funcionamento da operação semigrupo da distribuição Gaussiana.

O funcionamento do semigrupo

Nosso tipo de dados Gaussiano é definido como:

data Gaussian datapoint = Gaussian
    { n  :: !Int         -- The number of samples trained on
    , m1 :: !datapoint   -- The mean (first moment) of the trained distribution
    , m2 :: !datapoint   -- The variance (second moment) times (n-1)
    , dc :: !Int         -- The number of "dummy points" that have been added
    }

Para podermos estimar uma Gaussiana a partir de uma amostra, é preciso encontrar o número total de amostras (n), a média (m1) e a variação (calculada a partir de m2). (Explicaremos o que significa dc daqui a pouco) Portanto, temos de descobrir uma definição adequada para a nossa operação semigrupo abaixo:

(Gaussian na m1a m2a dca) <> (Gaussian nb m1b m2b dcb) = Gaussian n' m1' m2' dc'

Primeiro, a gente calcula o número de amostras n’. O número de amostras na distribuição resultante é simplesmente a soma do número de amostras em ambas as distribuições de entrada:

Depois, calculamos a nova média m1′. Começamos com a definição de que a média (?) final é:

Então, nós separamos o somatório como se o elemento de entrada xi fosse da Gaussiana esquerda a ou da Gaussiana direita b, e substituímos com a definição da média acima:

Observe que isso é simplesmente a média ponderada das duas médias. Isso, intuitivamente, faz sentido. Mas existe um pequeno problema com essa definição: quando implementada em um computador com aritmética de ponto flutuante, nós teremos sempre o infinito quando n’ for 0. Resolvemos esse problema adicionando um elemento “fictício” para a Gaussiana sempre que n’ for zero. Isso aumenta n’ de 0 para 1, impedindo a divisão por 0. A variável dc conta ​​quantas variáveis fictícias foram adicionadas para que possamos removê-las antes de executar os cálculos (por exemplo, encontrar o pdf), que seriam afetados por um número incorreto de amostras.

Finalmente, devemos calcular o novo m2′. Começamos com a definição de que os tempos de variação (n-1) são:

(Note que a segunda metade da equação é uma propriedade de variação, e sua derivação pode ser encontrada na wikipedia).

Em seguida, nós fazemos um pouco de álgebra, dividimos os somatórios de acordo com qual entrada Gaussiana trouxe o ponto de dados, e substituímos novamente a definição de m2 para obtermos:

(Note que a segunda metade da equação é uma propriedade da variação e sua derivação pode ser encontrada na wikipedia).

Em seguida, nós fazemos um pouco de álgebra, dividir os somatórios de acordo com qual a entrada gaussiana o ponto de dados veio, e substituir novamente a definição de m2 para obter:

 

Observe que essa equação não possui divisões. É por isso que estamos armazenando m2 como os tempos de variação (n-1) em vez de simplesmente a variação em si. Adicionar as divisões extras faz com que o treinamento de nossa distribuição Gaussiana rode quatro vezes mais devagar. Eu diria que Haskell fica muito rápido se o número de divisões de ponto flutuante que que executamos está impactando tanto o desempenho do nosso código!

Desempenho

Essa interpretação algébrica da distribuição Gaussiana possui tempo e desempenho de espaço excelentes. Para mostrar isso, vamos comparar o desempenho com o excelente pacote Haskell chamado “statistics“, que também tem suporte para distribuições Gaussianas. Nós usamos o critério de pacote para criar três testes:

> size = 10^8
> main = defaultMain
>     [ bench "statistics-Gaussian" $ whnf (normalFromSample . VU.enumFromN 0) (size)
>     , bench "HLearn-Gaussian" $ whnf
>         (train :: VU.Vector Double -> Gaussian Double)
>         (VU.enumFromN (0::Double) size)
>     , bench "HLearn-Gaussian-Parallel" $ whnf
>         (parallel $ (train :: VU.Vector Double -> Gaussian Double))
>         (VU.enumFromN (0::Double) size)
>     ]

Nesses testes, nós calculamos o tempo de três métodos diferentes de construção de distribuições Gaussianas, dados 100.000.000 pontos de dados (?). No meu laptop, com dois núcleos, obtive estes resultados:

statistics-Gaussian	2.85 sec
HLearn-Gaussian	1.91 sec
HLearn-Gaussian-Parallel	0.96 sec

Show! O método algébrico conseguiu superar o método tradicional para o treinamento de uma distribuição Gaussiana por uma margem útil. Além disso, nosso algoritmo paralelo é executado exatamente duas vezes mais rápido em dois processadores. Teoricamente, isso deve escalonar para um número arbitrário de processadores, mas eu não tenho uma máquina melhor para experimentar.

Outra vantagem interessante da biblioteca HLearn é que nós podemos negociar o tempo e espaço de desempenho, alterando as estruturas de dados que armazenam o nosso conjunto de dados. Especificamente, podemos usar as mesmas funções para treinar uma lista ou um vetor unboxed. Fazemos isso usando o pacote ConstraintKinds em hackage que estende as classes básicas tipo Functor e Foldable para trabalhar em classes que requerem constraints. Assim, temos um exemplo de uma instância Functor de Vector.Unboxed. Isso não é possível sem ConstraintKinds.

Usando este código benchmark:

main = do
    print $ (train [0..fromIntegral size::Double] :: Gaussian Double)
    print $ (train (VU.enumFromN (0::Double) size) :: Gaussian Double)

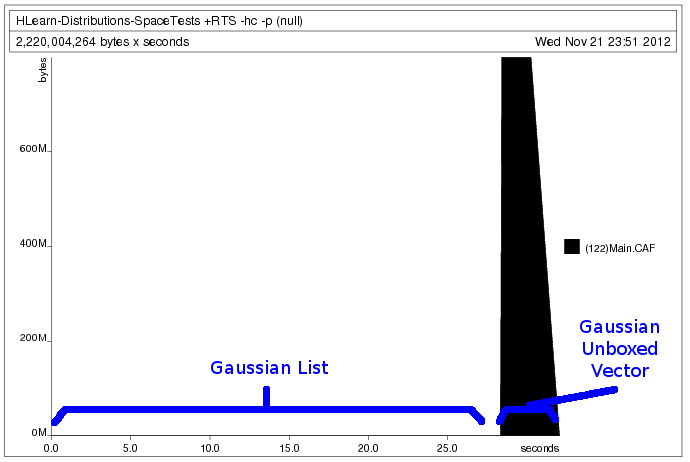
Nós geramos o seguinte perfil heap:

O processamento dos dados como um vetor exige que a gente aloque toda a memória com antecedência. Isso permite que o programa rode mais rápido, mas nos impede de carregar conjuntos de dados maiores do que a quantidade de memória que temos. O processamento dos dados como uma lista, no entanto, nos permite alocar a memória apenas como a usamos. Mas porque as listas são estruturas de dados encaixotadas e preguiçosas, temos que aceitar que o nosso programa será executado cerca de 10x mais lento. Para a nossa sorte o GHC cuida de todos os detalhes chatos que fazem isso acontecer sem problemas. Nós só temos que escrever a nossa função train uma vez.

Artigos futuros

Ainda há pelo menos mais quatro grandes tópicos para abordarmos na biblioteca HLearn: (1) Podemos estender essa discussão para mostrar como o algoritmo de aprendizagem NaiveBayes tem um monóide e uma estrutura de grupo semelhantes. (2) Existem muitos mais algoritmos de aprendizagem com estruturas de grupo em que podemos dar uma olhada. (3) Podemos observar exatamente como todas essas funções de ordem superior, como batch e parallel trabalham por baixo dos panos. E (4) podemos ver como a rápida semelhante que eu mencionei brevemente funciona e por que é importante.

***

Texto original disponível em http://izbicki.me/blog/gausian-distributions-are-monoids#comment-988