Operadores bitwise são utilizados quando precisamos realizar operações em nível de bits com números inteiros, ou seja, trabalhar com sua representação binária.
Caso ambos os operandos sejam strings, esses operadores irão trabalhar com os valores ASCII de seus caracteres.
Operações Bitwise
- Operador & ( Bitwise AND )
- Operador | ( Bitwise OR )
- Operador ^ ( Bitwise XOR )
- Operador ~ ( Bitwise NOT )
Bit Shift
- Operador >> ( Bitwise right shift )
- Operador << ( Bitwise left shift )
Não confunda os operadores bitwise com operadores lógicos, algumas representações são parecidas, mas suas funcionalidades são diferentes.
Operador & ( Bitwise AND )
O operador & ( Bitwise AND ) compara dois valores utilizando suas representações binárias, retornando um novo valor. Para formar esse valor de retorno, cada bit é comparado, retornando 1( true ) quando ambos os bits forem iguais a 1( true ); caso contrário, retorna 0( false ).
<?php $a = 5; // 00000101 $b = 1; // 00000001 // 00000101 // & 00000001 $c = $a & $b; // 00000001 var_dump($c); // Resultado: 1 ?>
Operador | ( Bitwise OR )
O operador | ( Bitwise OR ) compara dois valores utilizando suas representações binárias, retornando um novo valor. Para formar esse valor de retorno, cada bit é comparado, retornando 1( true ) se um dos bits comparados forem iguais a 1( true ); caso contrário, retorna 0 ( false ).
<?php $a = 5; // 00000101 $b = 3; // 00000011 // 00000101 // | 00000011 $c = $a | $b; // 00000111 var_dump($c); // Resultado: 7 ?>
Operador ^ ( Bitwise XOR )
O operador ^ ( Bitwise XOR ) compara dois valores utilizando suas representações binárias, retornando um novo valor. Para formar esse valor de retorno, cada bit é comparado, retornando 1( true ) quando os bits comparados forem diferentes; caso contrário. retorna 0( false ).
<?php $a = 5; // 00000101 $b = 3; // 00000011 // 00000101 // ^ 00000011 $c = $a ^ $b; // 00000110 var_dump($c); // Resultado: 6 ?>
Operador ~ ( Bitwise NOT )
O operador ~ ( Bitwise NOT ), diferente dos operadores anteriores, é um operador que afeta apenas um operando, incrementando(++) e invertendo seu sinal, de positivo para negativo e vice-versa.
<?php $a = -2; // 11111111111111111111111111111110 $a = ~$a; // 00000000000000000000000000000001 var_dump($a); // Resultado: 1 $b = 2; // 00000000000000000000000000000010 $b = ~$b; // 11111111111111111111111111111101 var_dump($b); // Resultado: -3 ?>
Aparentemente esse operador é o mais simples dos operadores bitwise, mas essa não é a explicação real desse operador, é apenas uma forma de calcular o resultado de maneira rápida e objetiva. O operador Bitwise NOT tem como função inverter cada um dos bits de um determinado valor em sua representação binária – isso muitas vezes causa confusão, já que costumamos trabalhar com os números binários usando apenas a parte que nos interessa. Por exemplo, no caso de um sistema 32bits, o valor 16 é representado por:
00000000000000000000000000010000 // A representação binária acima corresponde ao valor decimal 16
Como podemos observar, é uma representação longa para um valor baixo. Para facilitar o entendimento, costumamos trabalhar usando uma forma reduzida, por exemplo:
00010000 // A representação binária acima corresponde ao valor decimal 16
Mas para realmente entender o operador Bitwise NOT, precisamos trabalhar com sua representação completa, afinal esse operador, como foi explicado, inverte TODOS os bits. Caso seja utilizado o operador Bitwise NOT no valor 16, iremos inverter todos os seus bits em sua representação completa (32 bits, nesse caso):
00000000000000000000000000010000 // A representação binária acima corresponde ao valor decimal 16 11111111111111111111111111101111 // A representação binária acima corresponde ao valor decimal -17
O resultado será o valor -17, mas da onde saiu -17 se todos os bits ficaram 1( true ) e apenas a casa que representa o valor 16 está 0 (false)? Caso você não esteja muito familiarizado com números binários, o primeiro bit é responsável pelo sinal, 1( true ) representa números negativos e 0( false ) representa positivos. Sendo assim, o conceito de true e false muda, os bits marcados com zero passam a representar o valor negativo. No resultado anterior, temos o valor 0( false ) na casa que representa o valor 16, isso indica -1 com -16, formando o resultado -17.
O número 0 ( zero ) é considerado positivo, logo o primeiro valor dos negativos é -1:
11111111111111111111111111111111 // A representação binária acima corresponde ao valor decimal -1
O operador >> ( deslocamento de bits para a direita ), olhando pela base decimal, parece estranho, mas se olharmos pela representação binária do valor, iremos identificar facilmente que os bits deslizam para direita, sendo o operando da direita responsável pelo número de vezes que os bits serão deslizados. Cada passo equivale a dividir por 2, ou seja, $a >> 3, é o mesmo que dividir $a por 2 três vezes.
<?php $a = 45; // 00101101 $b = $a >> 3; // 00000101 var_dump($b); // Resultado: 5 ?>
Operador << ( Bitwise left shift )
O operador << ( deslocamento de bits para a esquerda ) segue a mesma linha de raciocínio do operador >>, mas ao invés de deslizar os bits para a direita, desliza os bits para a esquerda. Cada passo equivale a multiplicar por 2, ou seja, $a << 3, é o mesmo que multiplicar $a por 2 três vezes.
<?php $a = 5; // 00000101 $b = $a << 3; // 00101000 var_dump($b); // Resultado: 40 ?>
Como podemos observar, 45 >> 3 é igual a 5, mas 5 << 3 é igual a 40, isso porque quando utilizamos o Bitwise right sift, onde cada passo representa uma divisão por 2, o resto dessas divisões será ignorado, porque estamos trabalhando com valores inteiros.
<?php $a = 45; // $a = $a >> 3; $a = $a / 2; var_dump($a); // float 22.5 var_dump((int) $a); // int 22 $a = $a / 2; var_dump($a); // float 11.25 var_dump((int) $a); // int 11 $a = $a / 2; var_dump($a); // float 5.625 var_dump((int) $a); // int 5 ?>
Trabalhando com operadores bitwise no PHP
Agora que conhecemos um pouco mais sobre operadores bitwise, vamos utilizá-los para extrair os valores RGB de uma cor (representação hexadecimal), transformar valores RGB em hexadecimal e por último simular um controle de acesso utilizando operadores bitwise.
Convertendo uma cor( Hexadecimal ) para valores RGB
<?php
// #9bb226
// DEC: 10203686
// BIN: 100110111011001000100110
$color = 0x9bb226;
// 000000000000000010011011
// & 11111111
$r = ($color >> 16) & 0xFF;
// 10011011
// 000000001001101110110010
// & 11111111
$g = ($color >> 8) & 0xFF;
// 10110010
// 100110111011001000100110
// & 11111111
$b = $color & 0xFF;
// 00100110
printf("Red: %d, Green: %d, Blue: %d", $r, $g, $b);
// Resultado
// Red: 155 Green: 178 Blue: 38
?>
O processo para converter uma cor em formato hexadecimal para RGB se baseia em dividir o valor hexadecimal em três pares, confira na imagem abaixo:
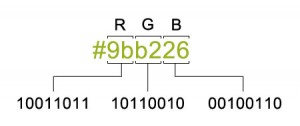
No exemplo acima, utilizamos dois operadores bitwise para realizar esse processo: Bitwise right shift, que possibilitou o posicionamento correto dos valores binários em cada momento, e Bitwise AND, que filtrou o valor binário obtido, deixando apenas os bits que seriam necessários para representar cada um dos valores(RGB).
Convertendo valores RGB para hexadecimal
<?php
$r = 155;
$g = 178;
$b = 38;
$color = ($r << 16) | ($g << 8) | $b;
printf("Cor: #%x", $color);
// Resultado
// Cor: #9bb226
?>
Desta vez, realizamos o processo invertido, basicamente unindo os bits que foram separados anteriormente.
Controle de acesso utilizando operadores bitwise
<?php
define('READ', 1);
// 00000001
define('WRITE', 2);
// 00000010
define('EDIT', 4);
// 00000100
define('DELETE', 8);
// 00001000
$thiago = 1; // READ = 1
// 00000001
$claudio = 3; // READ + WRITE = 3
// 00000011
$diogo = 15; // READ + WRITE + EDIT + DELETE = 15
// 00001111
$permission = ($thiago & READ) ? 'Sim' : 'Não';
printf("Thiago pode ler? %s", $permission);
// Resultado: Thiago pode ler? Sim
echo PHP_EOL . '<br />';
$permission = ($thiago & EDIT) ? 'Sim' : 'Não';
printf("Thiago pode editar? %s", $permission);
// Resultado: Thiago pode editar? Não
echo PHP_EOL . '<br />';
$permission = ($claudio & WRITE) ? 'Sim' : 'Não';
printf("Claudio pode escrever? %s", $permission);
// Resultado: Claudio pode escrever? Sim
echo PHP_EOL . '<br />';
$permission = ($claudio & DELETE) ? 'Sim' : 'Não';
printf("Claudio pode deletar? %s", $permission);
// Resultado: Claudio pode deletar? Não
echo PHP_EOL . '<br />';
$permission = ($diogo & EDIT) ? 'Sim' : 'Não';
printf("Diogo pode editar? %s", $permission);
// Resultado: Diogo pode editar? Sim
echo PHP_EOL . '<br />';
$permission = ($diogo & DELETE) ? 'Sim' : 'Não';
printf("Diogo pode deletar? %s", $permission);
// Resultado: Diogo pode deletar? Sim
?>
No exemplo acima, primeiro definimos quatro constantes que representam os níveis de acesso, com valores “estratégicos” para o funcionamento do controle de acesso. Como podemos perceber, cada valor ocupa uma casa única em sua representação binária, depois definimos três variáveis, simulando três usuários, onde $thiago só tem permissão de leitura, logo seu perfil terá valor 1; $claudio possui permissão para leitura e escrita, tendo como valor 3 e $diogo tem todas permissões, tendo como valor 15. O que estamos fazendo aqui é acumular os valores de cada nível de acesso e, graças aos valores estratégicos, apenas acumulamos bits na representação binária. No restante do script, efetuamos diversas comparações utilizando o operador Bitwise AND, que como vimos no início do artigo retorna 1( true ) quando ambos os bits forem iguais a 1( true ), caso contrário retorna 0( false ), ou seja, se o usuário não tiver determinado nível de acesso, o resultado será 0( false ), pois não teremos bits iguais.
O operador ternário é utilizado para verificar se existe resultado na comparação do usuário (perfil) com o nível de acesso; quando o resultado for diferente de 0 ( false ), nossa variável $permission terá como valor “Sim”, informando que o usuário tem permissão de acesso. Caso o usuário não tenha acesso ao nível comparado e retornar 0 ( false ), o valor de $permission será “Não”.
$var = (<condição>) ? <verdadeiro> : <falso>;
Neste artigo, utilizamos todos os exemplos baseado em sistemas 32bits – caso você trabalhe utilizando sistemas 64 bits, que como o nome já diz, suportam 64 bits, algumas das representações acima podem ser diferentes.
000000000000000000000000000000000000000000000000000000000000100 // A representação binária acima corresponde ao valor decimal 4 111111111111111111111111111111111111111111111111111111111111111 // A representação binária acima corresponde ao valor decimal -1 111111111111111111111111111111111111111111111111111111111111011 // A representação binária acima corresponde ao valor decimal -5



