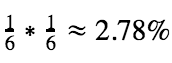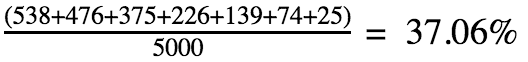Ultimamente, temos usado uma abordagem mais probabilística do que determinística para gerenciar nossos processos. Isso significa que usamos diferentes métodos estatísticos para prever o futuro ao invés de estimativas cegas. Mas… imprevisibilidade não era exatamente uma das razões de termos mudado de Waterfall para Ágil?
Sim, imprevisibilidade é inerente ao desenvolvimento de software. Seria impossível prever todas as features de um sistema no começo de um projeto, por exemplo.
Mas e se nós pudéssemos prever como as próximas semanas se comportariam? Isso é o que tentamos alcançar ao compilar métricas e rodar simulações de Monte Carlo.
Para entender mais sobre as métricas que utilizamos, veja:
- Why we love metrics? Learning with lead time
- Why we love metrics? Throughput and burnup charts
- Why we love metrics? Cumulative flow diagrams
A maioria das pessoas não usa métrica alguma para gerenciar projetos. Então, imagine quantas usam modelos estatísticos complexos para prever o fim de um projeto. No entanto, aplicar esse conhecimento em seu projeto ajudará a entregar mais rápido e melhor.
Neste artigo, você verá como evoluímos de uma abordagem ingênua de predição para uma mais precisa e robusta, utilizando a simulação de Monte Carlo. Mais ainda, explicarei de uma maneira fácil como esta simulação funciona, fazendo analogia entre um jogo de dados e projeto de desenvolvimento de software. Saber quando o projeto, provavelmente, vai acabar, pode ajudar você a gerenciar as despesas da empresa, melhorar feedbacks a stakeholders e passar mais confiança de que você está no controle do projeto.
Por que não outros métodos?
Nós passamos por diferentes métodos de predição desde o início da empresa, e todos eles tinham algum ponto fraco. Aqui, listei alguns deles e o porque optamos por abandoná-los.
Throughput médio
Alguns podem pensar em um método simples, no qual usaria o throughput médio para prever o final de um projeto. No entanto, como você pode ver neste artigo, Power of the metrics: Don’t use average to forecast deadlines, isso seria um método ingênuo e não funcionaria.
Regressão linear
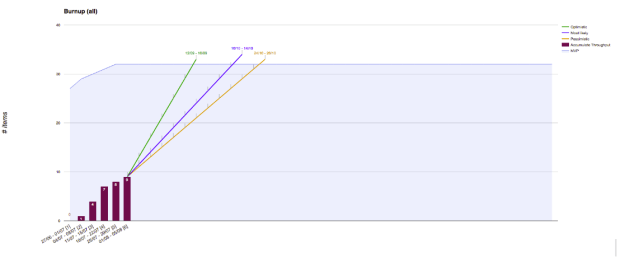
Este foi nosso primeiro método. Regressão linear baseada no throughput acumulado para prever quando um projeto seria finalizado:
No entanto, identificamos dois pontos diferentes que não estávamos considerando quando fazíamos esse tipo de análise:
- Nós mantínhamos o número de itens no backlog constante para que a predição funcionasse, o que causa muito viés.
- Nós descobrimos, depois de algumas análises, que tanto o nosso throughput, quanto o lead times não seguem distribuição normal, portanto, não faz sentido calcular regressão linear (veja em Looking at Lead Time in a different way e Assumptions of Linear Regression)
Configuração manual
Primeiramente, focamos em evitar erros estatísticos, como o caso da regressão linear. Começamos a utilizar um modelo mais compreensível, que usa métodos que sabemos que estão enviesados, mas que podemos controlar de acordo com o contexto do projeto.
Adicionamos manualmente diferentes retas de predições de throughput baseados em percentis do histórico do projeto.
Nós tivemos melhores resultados com isso, já que podíamos mudar a previsão manualmente e, portanto, ajustá-la de acordo com o contexto específico do projeto. Porém, o fato de desconsiderarmos mudanças no backlog, nos motivou a dar um passo a mais e testar simulações de Monte Carlo.
Simulação de Monte Carlo
Wikipedia define Monte Carlo como:
Qualquer método de uma classe de métodos estatísticos que se baseiam em amostragens aleatórias massivas para obter resultados numéricos, isto é, repetindo sucessivas simulações um elevado número de vezes, para calcular probabilidades heuristicamente.
Pode parecer complexo ou difícil inicialmente, mas é muito mais simples do que parece. Você pode considerar que é o método de força bruta das previsões. Vou apresentar um simples exemplo, e então, mostrar como nós aplicamos na vida real. Existe uma simulação feita por Larry Maccherone, que pode facilitar o entendimento ainda mais.
Jogo de dados
Imagine que você está jogando um jogo de dados, no qual o objetivo é alcançar a soma de 12 pontos com o menor número de jogadas. A melhor jogada, no caso, seria jogar 2 dados consecutivos, nos quais você tiraria o número 6 em ambos. A pior seria jogar o dado 12 vezes e caísse no 1 todas as vezes. O que queremos calcular com Monte Carlo é a probabilidade de finalizar o jogo depois de N rodadas.
Considerando que temos 6 possíveis resultados para cada jogada de dado (6 faces) qual é a probabilidade de terminar o jogo na primeira rodada? Zero. Já que é impossível tirar 12 pontos se o dado vai até 6. E na segunda rodada? É a probabilidade de conseguir dois 6 consecutivos, e que, em estatística básica, é:
E na terceira rodada?
Você pode alcançar 12 pontos de diferentes maneiras: (3,3,6), (3,4,5), (3,5,4), (3,4,6), (5,5,2), (4,4,4) etc. Agora, o cálculo estatístico não são tão fáceis, certo? É aí que entra a simulação de Monte Carlo.
O que Monte Carlo faz é simular milhares de rodadas de dados, para então, analisar o resultado. Por exemplo, para saber a probabilidade de terminar o jogo na terceira rodada, a simulação rodaria o dado três vezes, somaria os pontos, e guardaria o resultado. Depois disso, iria repetir esses passos 5000 vezes e resumir quantas rodadas cada soma de pontos obteve:
| SOMA DE 3 RODADAS | QUANTAS VEZES APARECEU |
|---|---|
| 3 | 21 |
| 4 | 70 |
| 5 | 134 |
| 6 | 240 |
| 7 | 370 |
| 8 | 509 |
| 9 | 581 |
| 10 | 586 |
| 11 | 636 |
| 12 | 538 |
| 13 | 476 |
| 14 | 375 |
| 15 | 226 |
| 16 | 139 |
| 17 | 74 |
| 18 | 25 |
Agora, o algoritmo soma todas as ocorrências que geraram soma maior do que 12 e divide o resultado pelo número total de ocorrências (5000). Neste caso:
O mesmo que fizemos para o terceiro round, faríamos para o quarto, quinto etc.
Mundo real
A solução do mundo real é muito similar ao exemplo dos dados. A única diferença é que o objetivo varia também (os 12 pontos no cenário do jogo), para considerar mudanças no backlog.
Então, o possível resultado de cada rodada (os lados do dado) são o histórico de throughput. E, do mesmo jeito que nós “rodamos dados” para o throughput, nós precisamos rodar os dados para o backlog, para dar chances do mesmo crescer também. Nesse caso, os possíveis resultados são chamados de Backlog Growth Rates (BGR).
Comecemos devagar. Digamos que nosso histórico do projeto é o seguinte:
| NÚMERO DA SEMANA | HISTÓRICO DO THROUGHPUT | HISTÓRICO DO BACKLOG |
|---|---|---|
| 1 | 2 stories | 15 stories (BGR: 0) |
| 2 | 3 stories | 17 stories (BGR: 2) |
| 3 | 0 stories | 18 stories (BGR: 1) |
| 4 | 2 stories | 19 stories (BGR: 1) |
| 5 | 5 stories | 21 stories (BGR: 2) |
| 6 | 0 stories | 22 stories (BGR: 1) |
| 7 | 1 stories | 22 stories (BGR: 0) |
| 8 | 3 stories | 24 stories (BGR: 2) |
| 9 | 3 stories | 24 stories (BGR: 0) |
Então, as possíveis jogadas para cada rodada de throughput seria o conjunto {2,3,0,2,5,0,1,3,3} e para backlog seria {0,2,1,1,2,1,0,2,0}. Não excluímos números repetidos, pois com eles mantemos a maior probabilidade de sair esses números, ao invés de outros.
Podemos aplicar o mesmo racional que está por trás do jogo dos dados. Qual a probabilidade do throughput acumulado alcançar a mesma quantidade que o backlog, ou mais, na primeira semana? Alguns dos possíveis resultados são os seguintes:
| RODADA DE THROUGHPUT | RODADA DE BGR | SOMA DE THROUGHPUT | SOMA DO BACKLOG |
|---|---|---|---|
| 2 | 0 | 19+2 = 21 | 24 + 0 = 24 |
| 2 | 2 | 19+2 = 21 | 24 + 2 = 26 |
| 2 | 1 | 19+2 = 21 | 24 + 1 = 25 |
| 3 | 0 | 19+3 = 22 | 24 + 0 = 24 |
| 3 | 2 | 19+3 = 22 | 24 + 2 = 26 |
| 3 | 1 | 19+3 = 22 | 24 + 1 = 25 |
| 0 | 0 | 19+0 = 19 | 24 + 0 = 24 |
| 0 | 2 | 19+0 = 19 | 24 + 2 = 26 |
Então, rodaríamos muitos como esses e veríamos quantos deles tem soma de throughput maior do que a soma do backlog, e dividiríamos o resultado pelo número de simulações. Fazendo isso, teríamos a probabilidade do projeto ser finalizado na primeira semana. Para a próxima semana, nós faríamos a mesma coisa, mas rodando dois dados em cada simulação (dois para BGR e dois para throughput) somando-os.
Um problema que esse método tem é que o backlog, no começo do projeto, se comporta diferente do que no meio ou final do mesmo. No começo, o backlog cresce muito mais rápido, pois estamos tendo melhor conhecimento dos problemas e nuances do projeto. Já no final, o crescimento é de basicamente por causa de refinamento de histórias.
Para resolver este problema, ao invés de considerar todo o histórico de backlog para os cálculos, nós consideramos apenas os últimos 10 pontos, o que nos dá melhor perspectiva de como o backlog está se comportando ultimamente.
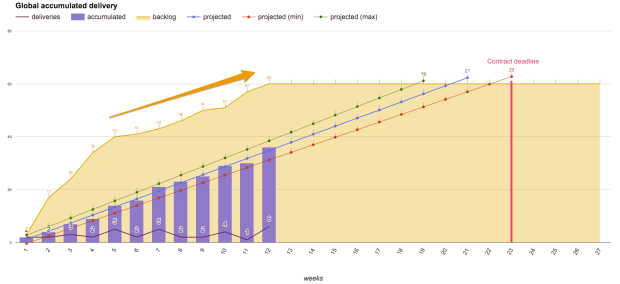
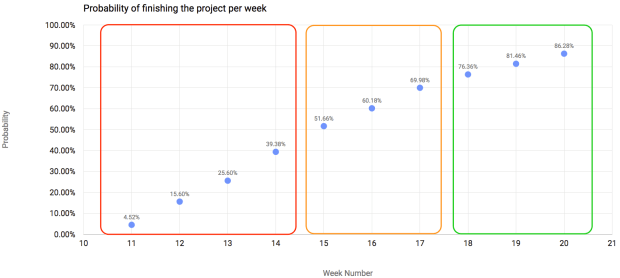
O resultado para as próximas 10 semanas, utilizando a abordagem acima, é representada no gráfico:
Como podem ver, realcei três áreas do gráfico para ilustrar o que poderia ser o entendimento do mesmo:
- A primeira área, a vermelha, são as semanas nas quais temos 50% ou menos probabilidade de terminar o projeto. O que significa que seria arriscado demais dizer aos stakeholders que seu projeto seria finalizado nessas 4 semanas.
- A próxima área, laranja, ilustra as semanas que têm probabilidade entre 50% e 75% de terminar o projeto. Eu diria que, se os stakeholders estão te pressionando para entregar rápido, seria possível terminar nessas semanas, mas alguns ajustes de processos seriam necessários.
- A área verde é a mais livre de riscos, onde a probabilidade de terminar o projeto é maior do que 75%. Eu sugiro que você sempre dê preferência para estimar o fim do seu projeto baseado nesta área. No entanto, sabemos que nem sempre podemos ser tão flexíveis assim.
Nós testamos Monte Carlo em projetos passados, e parece funcionar muito bem, no entanto, como em todo método estatístico, ele se torna melhor depois de algumas semanas que o projeto já começou, por ter mais dados para trabalhar.
Conclusão
Prever quando um projeto irá acabar parece muito mágico, mas este método é extremamente simples de ser implementado; aumenta nosso entendimento e predição em relação ao projeto. É importante deixar claro que este método é estatístico e heurístico, portanto, não é a prova de falha. O objetivo principal é adicionar mais um elemento ao seu conjunto de ferramentas e deixar o gerenciamento de projetos um pouco mais fácil.
Para executar simulações sem muito trabalho, disponibilizamos uma versão simples da nossa planilha para você baixar.
Se quiser aprender mais sobre simulações de Monte Carlo, recomendo essas referências:
- Troy Magennis – Forecasting and Simulating Software Development Projects: Effective Modeling of Kanban & Scrum Projects using Monte-carlo Simulation
- Daniel Vacanti e seus website, livro e blog: Actionable Agile
- Joel Spolsky’s blog post on Evidence Based Scheduling
Como você faz sua projeção de fim de projeto? Qual sua opinião sobre nossa abordagem? Compartilhe seus pensamentos conosco nos comentários abaixo!
***
Planilha com Simulação de Monte Carlo
***
Este artigo foi publicado originalmente em: http://blog.plataformatec.com.br/2017/06/por-que-usamos-simulacoes-de-monte-carlo-para-gerenciar-projetos/