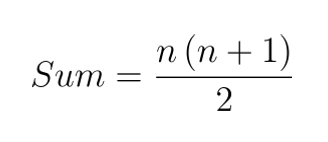Como aumentar o desempenho de uma função Swift para ser 10 milhões de vezes mais rápida

Descubra como um matemático do século XIX transformou o desempenho de um algoritmo de jogos do século XXI

Como desenvolvedores, estamos constantemente buscando maneiras de otimizar nosso código. Às vezes, as otimizações mais poderosas vêm de ideias aparentemente simples.

Hoje, vou compartilhar uma história fascinante sobre Carl Friedrich Gauss, um matemático do século XIX, e mostrar como sua fórmula aritmética pode melhorar drasticamente o desempenho em Swift — tanto em cenários teóricos quanto no mundo real.

Prepare-se, porque ao final deste artigo, você entenderá a mágica da fórmula de Gauss.

Imagine que você precisa calcular a soma de todos os números inteiros de 1 até n. É um problema clássico com várias maneiras de resolvê-lo. Para demonstrar, escrevi três funções em Swift:

1 — Loop For-In

Esta é a abordagem mais direta. Iteramos por cada número de 1 até n e os somamos:

func sumFromOneForIn(upto n: Int) -> Int {
   var result = 0
   for i in 1...n {
      result += i
   }
   return result
}

2 — Método Reduce

As capacidades de programação funcional do Swift nos permitem usar o método reduce para somar os números em um intervalo:

func sumFromOneReduce(upto n: Int) -> Int {
   return (1...n).reduce(0, +)
}

3 — Fórmula de Gauss

Agora, vamos apresentar a estrela do nosso show — a fórmula de Gauss. Quando criança, Gauss descobriu de forma inteligente que a soma dos números de 1 até n pode ser calculada com esta simples equação

Traduzindo para Swift, fica assim:

func sumFromOneGaussFormula(upto n: Int) -> Int {
   return (n * (n + 1)) / 2
}

Testando o Desempenho

Para medir como esses métodos se comportam, usei a API DispatchTime do Swift para calcular os tempos de execução em nanossegundos. Aqui estão os resultados para n = 1.000.000:

let n = 1_000_000
let timeForIn = SumCalculator.measureExecutionTime(of: SumCalculator.sumFromOneForIn, upto: n)
let timeReduce = SumCalculator.measureExecutionTime(of: SumCalculator.sumFromOneReduce, upto: n)
let timeGaussFormula = SumCalculator.measureExecutionTime(of: SumCalculator.sumFromOneGausFormula, upto: n)

print("For-In: \(timeForIn) ns")
print("Reduce: \(timeReduce) ns")
print("Formula: \(timeGaussFormula) ns")

Quem é o mais rápido?

Antes de mergulharmos na comparação de desempenho, vamos discutir brevemente a notação Big-O — um conceito fundamental em ciência da computação que nos ajuda a avaliar a eficiência de um algoritmo.

A notação Big-O descreve como o tempo de execução (ou uso de espaço) de um algoritmo cresce em relação ao tamanho da entrada. É expressa em termos de n, onde n representa o tamanho dos dados de entrada.

Por exemplo:

O(1): Tempo constante. O desempenho do algoritmo não depende de n.
O(n): Tempo linear. O tempo de execução cresce proporcionalmente a n.
O(n²): Tempo quadrático. O tempo de execução cresce exponencialmente à medida que n aumenta.

Método Reduce: Embora use programação funcional, internamente ele também itera pelo intervalo, dando a mesma complexidade O(n) do loop For-In.

Fórmula de Gauss: Este é o vencedor claro. Graças à sua complexidade de tempo constante O(1), ele calcula a soma diretamente usando uma única operação aritmética, independentemente do valor de n.

Para n = 1.000.000, essa diferença é gritante. O loop For-In e o método Reduce levam milhões de nanossegundos, enquanto a fórmula de Gauss conclui em apenas uma fração desse tempo.

Ao utilizar um algoritmo mais inteligente, alcançamos não apenas um desempenho melhor, mas também escalabilidade, tornando a fórmula de Gauss uma solução ideal para somar sequências ou problemas semelhantes.

Execution time of ForIn: 172266625 nanoseconds
Execution time of Reduce: 195087334 nanoseconds
Execution time of GaussFormula: 209 nanosecondsAverage execution time of ForIn: 170162783 nanoseconds
Average execution time of Reduce: 173793275 nanoseconds
Average execution time of GaussFormula: 16 nanoseconds

O tempo médio de execução:

Fórmula de Gauss: 16 nanossegundos (0,000000016 segundos)
Reduce ou For-In: 170.000.000 nanossegundos (0,17 segundos)

Com a fórmula de Gauss, o tempo de execução da função foi 10.625.000 vezes mais rápido.

Aplicação no Mundo Real: Pontuações em Leaderboards

Vamos passar da teoria para a prática. Estou desenvolvendo um aplicativo de jogos onde os jogadores acumulam pontos à medida que progridem pelos níveis. Para exibir um leaderboard, é preciso calcular a pontuação total até um específico nível n.

Aqui está como posso resolver isso usando as mesmas três abordagens (déjà vu):

1 — Usando um Loop (Abordagem Ingênua)

func cumulativeScoreLoop(scores: [Int], upto level: Int) -> Int {
   var total = 0
   for i in 0..<min(level, scores.count) {
      total += scores[i]
   }
   return total
}

2 — Usando Reduce (Abordagem Funcional)

Soma as pontuações com o reduce do Swift:

func cumulativeScoreReduce(scores: [Int], upto level: Int) -> Int {
   return scores.prefix(level).reduce(0, +)
}

3 — Usando a Fórmula de Gauss (Otimizada)

Se as pontuações são previsíveis (como 1, 2, 3, …), podemos calcular o total diretamente:

func cumulativeScoreGaussFormula(upto level: Int) -> Int {
   return (level * (level + 1)) / 2
}

Comparação de Desempenho

Com 1.000.000 de níveis, a fórmula de Gauss supera significativamente os métodos de loop e reduce.

Bônus (aplicação prática): Encontrando Números Faltantes

Aqui está outro caso de uso prático: detectar um número faltante em uma sequência. Suponha que você tenha uma sequência de números de 1 a n, mas um número está faltando.

Calculando a soma esperada usando a fórmula de Gauss e subtraindo a soma real, você pode encontrar o número faltante instantaneamente.

func findMissingNumber(_ nums: [Int], upto n: Int) -> Int {
    let expectedSum = (n * (n + 1)) / 2
    let actualSum = nums.reduce(0, +)
    return expectedSum - actualSum
}

let nums = [1, 2, 4, 5] // Missing 3
let missingNumber = findMissingNumber(nums, upto: 5)
print("Missing number: \(missingNumber)") // Output: 3

LEIA TAMBÉM

• 10 bibliotecas que todo desenvolvedor iOS deve substituir ainda em 2024
• React Native 0.76: o futuro do desenvolvimento mobile
• Aplicações Web e Mobile com a IDE online Bubble