A grosso modo podemos dividir a Estatística em três áreas:
- Estatística Descritiva
- Probabilidade
- Inferência Estatística
Estatística Descritiva é, em geral, utilizada na etapa inicial da análise, quando tomamos contato com os dados pela primeira vez.
Probabilidade pode ser pensada como a teoria matemática utilizada para se estudar a incerteza oriunda de fenômenos de caráter aleatório.
Inferência Estatística é o estudo de técnicas que possibilitam a extrapolação, a um grande conjunto de dados, das informações e conclusões obtidas a partir de subconjuntos de valores, usualmente de dimensão muito menor. [1]
Falando em Machine Learning, sabemos que em algum determinado momento o pesquisador vai ser deparar com problemas para analisar e entender um determinado conjunto de dados que possa ser relevante aos seu objeto de estudo. Ele necessita trabalhar os dados a fim de transformá-los em informações que possam ser comparadas com outros resultados, ou ainda para julgar sua adequação a alguma teoria estipulada para o problema.
Resumindo, a essência da Ciência é a observação e seu objetivo básico é a inferência que pode ser dedutiva ou indutiva. Quando falamos em estatística, a inferência estatística se trata da metodologia que objetiva a coleta, redução, análise e modelagem dos dados, a partir dos quais é possível fazer a inferência para uma população que nos permite chegar as previsões e assim tomar decisões. [2]
Ao falarmos Machine Learning falamos em estatística, e para ambos existe um elemento fundamental (você já deve ter notado na descrição acima): os dados. Quando olhamos para os dados precisamos notar o que há de mais especial, e geralmente conseguimos isso identificando nossas variáveis. Descobrir o porquê de uma determinada variação é um bom início para qualquer problema estatístico.
Uma variável é como uma pergunta que pode ter várias respostas possíveis.
Neste sentido vamos observar a tabela abaixo, que servirá de base para expressar os conceitos básicos que pretendo apresentar neste post:
| Nome | Idade |
|---|---|
| Machado de Assis | 69 |
| Carlos Drummond de Andrade | 85 |
| Graciliano Ramos | 61 |
| Mário Quintana | 38 |
| Guimarães Rosa | 59 |
Em nosso contexto, vamos considerar as linhas como observações/recursos, e as colunas vamos chamar de variáveis. As perguntas que nossas variáveis respondem são: “Qual o seu nome?” e “Qual a sua idade?”.
Primeira dica: Apenas o título da variável não representa toda sua história.
Como assim? O que vocêquer dizer com isso?
Se olharmos para a variável idade, não sabemos se ela se refere a idade do escritor hoje, a idade no momento de algum escrito famoso ou se foi a idade que ele tinha na época de seu falecimento.
Uma de nossas tarefas é investigar nossa fonte de dados em busca de compreender o verdadeiro significado de cada variável.
Outro ponto importante é saber identificar uma variável. Se neste contexto você me perguntar meu nome, vou te responder Vitor. Não importa quantas pessoas diferentes me perguntarem eu vou continuar respondendo Vitor. Neste caso meu nome não é uma variável, e sim uma constante.
Seguindo essa linha vamos ver que uma variável depende da pergunta que está sendo feita. A resposta para “Qual a ordem em que os dias da semana ocorrem” será uma constante. Sempre teremos a mesma ordem, terça sempre virá após a segunda e etc. Agora se pergunto “Que dia é hoje”, vamos ter como resposta uma variável, já que a resposta tem relação direta com o dia em que a pergunta é feita. “Que dia hoje” pode ser, segunda, terça, quarta… ou seja, teremos várias possíveis respostas corretas.
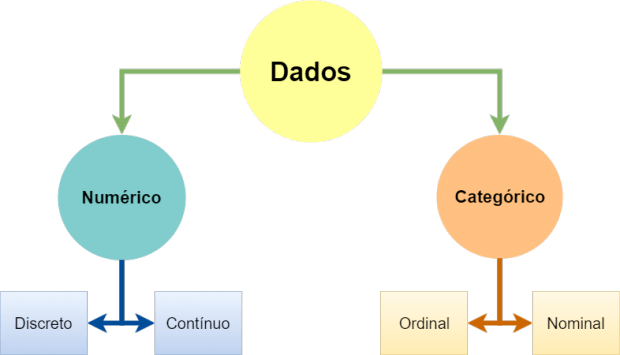
Variáveis numéricas e categóricas
Podemos diferenciar variáveis pelo tipo de dado. Em estatística consideramos dois tipos de variáveis: Númericas e Categóricas.
Variáveis podem ser classificadas da seguinte forma:
Variáveis Numéricas
São as características que podem ser medidas em uma escala quantitativa, ou seja, apresentam valores numéricos que fazem sentido. Podem ser contínuas ou discretas.
- Variáveis discretas: características mensuráveis que podem assumir apenas um número finito ou infinito contável de valores e, assim, somente fazem sentido valores inteiros. Geralmente são o resultado de contagens. Exemplos: número de filhos, número de bactérias por litro de leite, número de cigarros fumados por dia.
- Variáveis contínuas, características mensuráveis que assumem valores em uma escala contínua (na reta real), para as quais valores fracionais fazem sentido. Usualmente devem ser medidas através de algum instrumento. Exemplos: peso (balança), altura (régua), tempo (relógio), pressão arterial, idade.
Variáveis Categóricas
São as características que não possuem valores quantitativos, mas, ao contrário, são definidas por várias categorias, ou seja, representam uma classificação dos indivíduos. Podem ser nominais ou ordinais.
- Variáveis nominais: não existe ordenação dentre as categorias. Exemplos: sexo, cor dos olhos, fumante/não fumante, doente/sadio.
- Variáveis ordinais: existe uma ordenação entre as categorias. Exemplos: escolaridade (1o, 2o, 3o graus), estágio da doença (inicial, intermediário, terminal), mês de observação (janeiro, fevereiro,…, dezembro).
As distinções são menos rígidas do que a descrição acima nos apresenta.
Sendo assim, podemos definir que se o resultado a pergunta for numérica (“Qual a sua idade?”), então temos uma variável numérica. Se a reposta não pode ser representada de forma númerica (“Qual a raça do seu cachorro?”), então temos uma variável categórica.
Uma variável originalmente numérica pode ser coletada de forma categórica. Por exemplo, a variável idade, medida em anos completos, é quantitativa (contínua); mas, se for informada apenas a faixa etária (0 a 5 anos, 6 a 10 anos, etc…), é qualitativa (ordinal). Outro exemplo é o peso dos lutadores de boxe, uma variável quantitativa (contínua) se trabalhamos com o valor obtido na balança, mas qualitativa (ordinal) se o classificarmos nas categorias do boxe (peso-pena, peso-leve, peso-pesado, etc.).
Outro ponto importante é que nem sempre uma variável representada por números é quantitativa/numérica.
O número do telefone de uma pessoa, o número da casa, o número de sua identidade. Às vezes o sexo do indivíduo é registrado na planilha de dados como 1 se macho e 2 se fêmea, por exemplo. Isto não significa que a variável sexo passou a ser quantitativa!
Variáveis Ordinais
Geralmente vemos isso nos formulários e questionários que muitas vezes somos obrigados a responder. Geralmente essas pesquisar vem com opções como “Discordo Fortemente”, “Discordo”, “Neutro”, “Concordo” ou “Concordo Plenamente”. Estes dados têm uma estrutura especial, uma vez que refletem uma hierarquia, onde 0 representa o item de valor mais baixo, e 4 representa o item de valor mais alto.
- 0 = Discordo Totalmente
- 1 = Discordo
- 2 = Neutro
- 3 = Concordo
- 4 = Concordo Totalmente
Um primeiro cuidado em relação a codificação numérica é nunca destuir a hierarquia real dos dados. Se fizermos como está abaixo, nosso trabalho estará destruído.
- 0 = Discordo Totalmente
- 2 = Discordo
- 1 = Neutro
- 4 = Concordo
- 5 = Concordo Totalmente
Variáveis Nominais
Às vezes não há hierarquia em dados categóricos. Se a cor dos olhos foi codificada 0 “Azul” 1 “Verde” 2 “Castanhos”, temos que escolher aleatoriamente qual opção recebe qual número. Não importa se os olhos azuis são zero, ou um, ou dois, porque não há hierarquia na cor dos olhos.
Variáveis Discretas
Todas as variáveis contínuas são numéricas, mas nem todas as variáveis numéricas são contínuas.
“Quantas crianças você tem?” Não tem um número infinito de respostas, tem um número finito ou “discreto”. Você não pode ter 2,7 filhos, é 2 ou 3. Você pode estar pensando “Ok – números inteiros significa variável discreta”, mas isso é uma armadilha. E quanto à variável “tamanho do sapato”? Este é muitas vezes um número como 6,5 ou 10,5, mas não há um número infinito de tamanhos de sapato que existem, que seria o fim da fabricação de calçados como sabemos!
As variáveis discretas não precisam de codificação porque são numéricas
Variáveis Contínuas
Este conceito é difícil, mas você vai ficar bem porque já definimos o conceito de uma variável como resposta a uma pergunta .
Algumas perguntas têm um monte de respostas . Se você perguntar a 100 pessoas “Qual é o número da rua de sua casa?”, Você pode obter perto de 100 respostas diferentes. Isso é um pouco irritante, mas não vai quebrar seu software estatístico.
Algumas perguntas têm um número infinito de respostas . Literalmente, não existem números suficientes para capturar todas as possibilidades. Pode surpreender você saber quais variáveis se enquadram nesta categoria; Como altura, peso e idade.
Isto é porque 1,543 metros não é o mesmo que 1,5429 metros. Estes são números diferentes. 1.54299 é diferente novamente. Assim é 1.542999 metros. Acho que você vê o que estou dizendo, há um número ilimitado de números disponíveis para nós para representar a altura de alguém. O mesmo é verdade para peso e idade (e pressão arterial, e um monte de outras medições médicas). Na prática, estamos presos com um número mais limitado de opções, mas isso não muda o fato de que a própria variável tem possibilidades infinitas. Por favor, faça uma pergunta sobre isso nos comentários se você está confuso. Uma boa regra é que quase todas as medições são contínuas.
Quem se importa se uma variável é contínua? Você não precisa se importar muito frequentemente. Mas quando começamos a falar sobre a probabilidade de pesos e alturas particulares, esse detalhe teórico se torna extremamente importante.
As variáveis contínuas não exigem codificação, pois elas são sempre numéricas.
Codificando Variáveis
Eu não posso analisar diretamente uma sentença como “Hoje é terça-feira” em termos estatísticos. Quando nossa variável não é númerica, precisamos transformar cada resposta à nossa pergunta em um número, para que o mesmo possa ser analisado. Este processo de conversão é chamado de “codificação”. Como codificar uma variável vai depender do seu tipo de dado. Vou escrever um artigo específico sobre este conteúdo.
Referências
- [1] Noções de Probabilidade e Estatística – 6ª Edição Revista e Ampliada – Magalhães,Marcos Nascimento / Lima,Antonio Carlos Pedroso de Edusp
- [2] Estatística Básica – 8ª Edição Bussab,Wilton de Oliveira / Morettin,Pedro Alberto
Por hoje é só galera. Em breve devo publicar mais conteúdo direcionado as bases do Machine Learning.