As redes neurais revolucionaram o machine learning na última década, passando de uma área de pesquisa acadêmica relativamente obscura para um dos pilares da indústria, alimentando uma infinidade de aplicações nas quais grandes volumes de dados estão disponíveis.

A Uber usa redes neurais para um conjunto diversificado de aplicações, desde a construção de mapas do mundo baseados em modelos de visão computacional, até a resposta mais rápida do cliente usando o entendimento da linguagem natural para minimizar tempos de espera modelando padrões de demandas espaciais temporais entre cidades.

Em muitos casos, as redes neurais de maior sucesso empregam um grande número de parâmetros – de alguns milhões a centenas de milhões, ou mais – para alcançar o desempenho ideal. A boa notícia é que essas enormes redes geralmente funcionam muito bem, alcançando um desempenho impressionante em qualquer tarefa. Mas tais modelos são sistemas fundamentalmente complexos, impedindo o fácil entendimento devido ao grande número de parâmetros que são aprendidos sem intervenção humana.

No entanto, os esforços para entender o comportamento da rede persistem, porque à medida em que as redes afetam cada vez mais a sociedade, torna-se cada vez mais importante compreender seu funcionamento, e entender melhor os mecanismos e propriedades da rede irá acelerar a construção da próxima geração de modelos.

Em nosso artigo “Measuring the Intrinsic Dimension of Objective Landscapes“, na ICLR 2018, contribuímos para esse esforço contínuo desenvolvendo uma maneira simples de medir uma propriedade de rede fundamental, conhecida como dimensão intrínseca. No artigo, desenvolvemos a dimensão intrínseca como uma quantificação da complexidade de um modelo de uma maneira desacoplada de sua contagem de parâmetros brutos, e fornecemos uma maneira simples de medir essa dimensão usando projeções aleatórias.

Achamos que muitos problemas têm dimensões intrínsecas menores do que se poderia suspeitar. Usando a dimensão intrínseca para comparar domínios de problemas, medimos, por exemplo, que resolver o problema do pêndulo invertido é cerca de 100 vezes mais fácil do que classificar dígitos do MNIST, e jogar Atari Pong a partir de pixels é tão difícil quanto classificar o CIFAR-10.

Nossa abordagem e algumas descobertas interessantes estão resumidas no vídeo abaixo:

Abordagem básica

No treinamento típico da rede neural, instanciamos aleatoriamente os parâmetros de uma rede e depois os otimizamos para minimizar algumas perdas. Podemos pensar nessa estratégia como escolher um ponto inicial no espaço de parâmetros e, em seguida, seguir gradativamente os gradientes daquele ponto para um com uma perda menor.

Neste artigo, nós modificamos esse típico procedimento de treinamento: escolhemos o ponto inicial da mesma maneira, mas em vez de otimizar no espaço de parâmetro completo, geramos um subespaço aleatório em torno do ponto inicial e permitimos que o otimizador se mova apenas nesse subespaço. Construímos o subespaço aleatório, fazendo uma amostra de um conjunto de direções aleatórias a partir do ponto inicial; essas direções aleatórias são então congeladas durante o treinamento.

A otimização prossegue diretamente no sistema de coordenadas do subespaço. Computacionalmente, isso requer projeção do subespaço para o espaço nativo, e essa projeção pode ser alcançada de algumas maneiras diferentes. Algumas mais simples (projeção através de uma matriz aleatória densa) e outras mais complexas, porém, mais computacionalmente eficientes (projeção através de matrizes esparsas aleatórias construídas cuidadosamente ou através da transformação Fastfood).

Quão bem irá funcionar esse treinamento de projeção aleatória? Bem, isso depende inteiramente do tamanho do subespaço aleatório. Em um extremo, o uso de um subespaço aleatório unidimensional corresponde à pesquisa de linha em uma direção aleatória, e o uso de tal pesquisa provavelmente nunca levará a uma solução funcional. No outro extremo, se usarmos vetores aleatórios suficientes para abranger todo o espaço, é garantido que qualquer solução disponível do espaço original estará acessível.

A ideia principal desse trabalho é aumentar cuidadosamente a dimensão do subespaço até que as primeiras soluções sejam encontradas. À medida em que crescemos o espaço, geralmente observamos uma transição a partir de redes que não funcionam para aquelas que funcionam, e chamamos a dimensão na qual essa transição ocorre na dimensão intrínseca.

Nas seções a seguir, usamos essa abordagem para medir a dimensão intrínseca das redes usadas para resolver MNIST, variantes aleatórias do MNIST, CIFAR-10 e três tarefas de aprendizado por reforço (RL), reunindo algumas conclusões interessantes ao longo do caminho.

Medindo a dimensão intrínseca usando MNIST

Primeiro, treinamos uma rede de três camadas totalmente conectada (FC) com tamanhos de camada 784-200-200-10 para classificar o MNIST. Essa rede terá um espaço de parâmetro completo de cerca de 200 mil dimensões. Se medirmos sua dimensão intrínseca (veja o artigo para mais detalhes), obtemos apenas aproximadamente 750.

Uma conclusão saliente é que 750 é bastante pequeno. Em outras palavras, usando apenas 750 graus de liberdade, ou 0,4% do espaço total de parâmetros, podemos alcançar uma solução razoavelmente boa. O número de graus de liberdade requeridos (750) é muito menor do que o número de parâmetros que até mesmo um classificador linear de 10 classes implicaria (7840). De fato, 750 é ainda menor que o número de pixels de entrada (784), o que para o MNIST faz pelo menos algum sentido, já que muitos dos pixels de borda são pretos para cada exemplo no conjunto de dados.

Mas vamos pensar cuidadosamente sobre o que esse número 750 significa. Imagine que, em três dimensões, escolhemos uma linha unidimensional aleatória e conseguimos encontrar uma solução. Acontece que, nesse exemplo, a solução que encontramos deve ter pelo menos duas dimensões (mais precisamente: o coletor de solução quase certamente tem pelo menos duas dimensões).

Assim, no caso da nossa rede MNIST, se em 200 mil dimensões encontrarmos uma solução usando um subespaço de 750 dimensões, ela nos diz que a dimensão desse “blob” de soluções que encontramos deve ser de pelo menos 199.250. Em outras palavras, essa solução que encontramos é grande – ela tem muita redundância, ou é uma variedade com muitas direções, nas quais é possível viajar e ainda permanecer no conjunto de soluções. Legal, certo?

MNIST, mais largo ou mais alto

Em seguida, tentamos tornar nossa rede um pouco mais ampla, digamos, usando camadas ocultas com largura de 225, em vez de 200. Medir essa rede revela algo surpreendente: a dimensão intrínseca é mais ou menos a mesma: 750 (veja o artigo para medições precisas). Na verdade, ainda encontramos cerca de 750 se as camadas forem muito mais largas ou se adicionarmos mais camadas. Assim, parece que essa quantidade que estamos medindo é uma métrica bastante estável em uma família de modelos (ou pelo menos em toda essa família para esse conjunto de dados).

Mas o que a estabilidade dessa métrica nos diz?

Esta é uma das partes mais legais: adicionar mais parâmetros à rede revela características adicionais do panorama objetivo. Como a dimensão intrínseca não está mudando, isso significa que cada novo parâmetro que adicionamos – cada dimensão extra que adicionamos ao espaço de parâmetro nativo – vai diretamente para o conjunto de soluções. O parâmetro extra serve apenas para aumentar a redundância da solução definida por uma dimensão.

É claro que esse fenômeno nem sempre é válido para todas as famílias de redes e para todos os conjuntos de dados. Mas para esse conjunto de dados e família de rede, descobrimos que estamos em um patamar no espaço hiper parâmetro com dimensão intrínseca constante. No artigo, mostramos que esse patamar é bastante amplo, persistindo quando as camadas são ampliadas ou novas camadas são adicionadas.

Muitos pesquisadores notaram que redes maiores podem ser mais fáceis de treinar, e esse resultado sugere uma possível razão: à medida que adicionamos parâmetros, aumentamos o quanto o conjunto de soluções cobre o espaço. Há definitivamente algumas sutilezas aqui; então confira o artigo para advertências.

Compressibilidade do modelo

Podemos também considerar esses resultados a partir da perspectiva da compressibilidade. Para verificar e restaurar um desses modelos, precisamos armazenar apenas uma única semente para a criação de subespaço aleatório e, em seguida, os 750 parâmetros aprendidos.

Isso significa que o modelo pode ser compactado, nesse caso, a partir de seu espaço de parâmetro nativo de 200 mil por 250 vezes. Esse método de compactação não é necessariamente o mais eficiente, mas é bastante simples: qualquer modelo parametrizado de ponta a ponta pode ser treinado de ponta a ponta em um subespaço aleatório.

Podemos também pensar nessa abordagem como uma forma de limitar o comprimento mínimo de descrição (MDL) do modelo. Se você estiver familiarizado com a navalha de Occam, que afirma que a explicação mais simples é geralmente a melhor, o MDL é semelhante: sendo o restante igual, os modelos com MDL menor são os preferidos.

Redes neurais totalmente conectadas (FC) vs. convolucionais (CNNs)

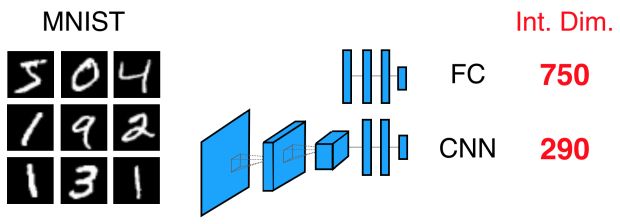
Se usarmos o mesmo conjunto de dados – MNIST – mas modelá-lo com uma rede convolucional, mediremos uma dimensão intrínseca muito menor que 290 (veja a Figura 1). Usando nosso argumento MDL, esse número menor sugere que as CNNs são melhores para classificar o MNIST do que as redes FC. Se você já trabalhou com redes neurais por um tempo, essa observação provavelmente não será uma grande surpresa para largar tudo e tuitar imediatamente este artigo (mas quem somos nós para te impedir?).

De fato, todos já reconhecem que as CNNs são ótimos modelos para classificação de imagens. Mas elas são sempre mais eficientes que as redes FC? E se nós treinássemos em uma versão do MNIST com pixels de entrada embaralhados, como feito em Zhang et al. (ICLR 2017)? Nesse caso, a rede FC invariante de permutação tem a mesma dimensão intrínseca de 750, como sempre, mas a CNN agora mede 1.400!

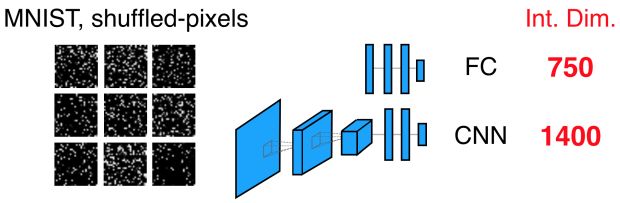
Assim, as CNNs são melhores até que a suposição de estrutura local seja quebrada, e após isso elas são consideravelmente piores na tarefa. Essas poucas conclusões podem ser intuitivas para os praticantes experientes, mas o ponto é que conseguimos obtê-las por medida, e não apenas por intuição. Em um mundo onde treinamos modelos maiores e maiores, consistindo de muitos submodelos treinados usando muitas perdas, projetar arquiteturas para submodelos pode ser bem menos óbvio. E, nesses casos, a capacidade de confiar na quantificação cuidadosa, e não na intuição excessiva pode ser muito útil.

Memorização aleatória de etiquetas

E se medirmos redes treinadas para memorizar etiquetas aleatoriamente embaralhadas, como feito em Zhang et al. (ICLR 2017)?

Acontece que uma rede treinada para memorizar cinco mil rótulos aleatórios em entradas MNIST requer uma dimensão intrínseca de 90 mil, que é muito maior do que a que observamos acima. Esse valor muito mais alto reflete a capacidade maior que a rede precisa para memorizar cada etiqueta aleatória, nesse caso, trabalhando com até 18 graus de liberdade para cada etiqueta memorizada.

Se nós treinamos nosso modelo para memorizar 50 mil rótulos aleatórios (10 vezes mais), a dimensão intrínseca cresce, mas na verdade não é muito: agora ela mede 190 mil. Isso é maior, mas não muito maior, exigindo apenas 3.8 graus de liberdade para cada etiqueta memorizada.

Esse é um resultado interessante, através do qual observamos um efeito semelhante à generalização, mas aqui é generalização de uma parte de um conjunto de treinamento aleatório para outra parte (também aleatória). Como os rótulos de todos os subconjuntos de dados são aleatórios, esse resultado não foi imediatamente esperado.

Parece que o treinamento em alguns rótulos aleatórios força a rede a configurar uma infraestrutura básica para a memorização, e que essa infraestrutura é usada para tornar a memorização posterior mais eficiente. O estudo futuro desse fenômeno em maior profundidade poderia produzir um trabalho interessante.

CIFAR-10 e ImageNet

Em nosso artigo, passamos um pouco mais de tempo no CIFAR-10 e no ImageNet, mas aqui vamos resumir brevemente os resultados.

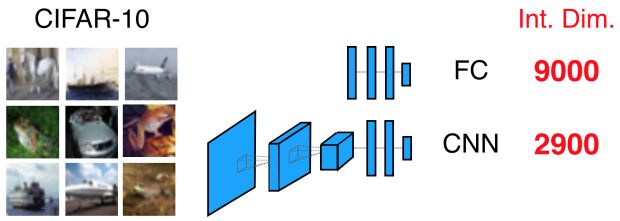
O CIFAR-10 é cerca de 10 vezes mais difícil do que o MNIST, com os modelos FC e CNN mostrando dimensões intrínsecas aproximadamente 10 vezes maiores. Como a dimensão de entrada do CIFAR-10 (3072) é apenas cerca de quatro vezes maior que a do MNIST (784), podemos atribuir essa complexidade adicional de classes no próprio conjunto de dados, por exemplo, imagens de aviões com maior variabilidade do que as do dígito 4.

Aprendizado por reforço

A abordagem de treinamento subespacial pode ser aplicada com a mesma facilidade nos cenários de aprendizado por reforço. De fato, a abordagem do subespaço aleatório foi motivada pelos resultados apresentados no artigo Evolutionary Strategies (ES) do OpenAI: que a aproximação de gradientes ao longo de um pequeno número de dimensões sugere que conjuntos de soluções são mais redundantes do que imaginávamos.

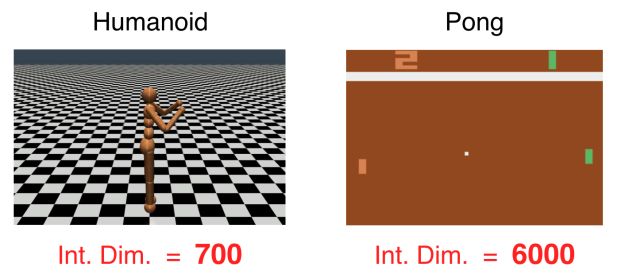
Conforme relatamos em nosso artigo, nós treinamos redes usando ES e Deep Q-Networks (DQN) e descobrimos que humanoides podem aprender a andar em cerca de 700 dimensões e que agentes podem jogar Atari Pong a partir de pixels em 6 mil dimensões.

Portanto, podemos dizer que essas tarefas exigem aproximadamente a complexidade de classificar MNIST e CIFAR-10, respectivamente. Essas dimensões relativamente baixas podem ser o motivo pelo qual a pesquisa aleatória e os métodos livres de gradiente funcionam tão bem quanto eles.

Finalmente, um último resultado que relatamos em nosso artigo é o problema do equilíbrio de pólos. Esse problema requer que um agente equilibre um pólo movendo o canto inferior esquerdo e direito. Embora esse problema possa ser desafiador para os seres humanos, uma vez que eles precisam reagir com rapidez suficiente para evitar que o pólo caia, para agentes simulados não sobrecarregados por reflexos lentos, esse problema é incrivelmente simples.

Na verdade, é solucionável com uma enorme dimensão intrínseca de: quatro. Isso parece quase comicamente fácil (~ 100 vezes mais fácil do que o MNIST), e essa simplicidade é algo que os pesquisadores devem ter em mente ao passar o tempo com problemas com brinquedos.

Próximos passos

Neste artigo, demonstramos uma maneira simples de medir a dimensão intrínseca, uma propriedade que fornece informações muito necessárias sobre a estrutura do panorama de perda das redes neurais e permite uma comparação quantitativa mais cuidadosa entre os modelos. Esperamos que essa medida seja útil em algumas direções.

Primeiro, fornece aos pesquisadores uma compreensão básica e de ordem de grandeza da complexidade dos problemas com os quais trabalham. Segundo, os pesquisadores podem se basear nesse trabalho, estendendo-se ao caso de projeções aleatórias não-lineares e não-uniformes, que podem fornecer limites mais rígidos ao modelo MDL.

Finalmente, esperamos que nossos aprendizados inspirem outros a encontrarem abordagens úteis para a escolha do melhor modelo ou submodelo para sua pesquisa. Se este trabalho lhe interessa e você gostaria de aprender mais, confira nosso artigo, use nosso código para medir suas próprias redes, e se você gostaria de trabalhar com esses tipos de desafios de pesquisa com o Uber AI Labs, candidate-se a um cargo em nosso time.

***

Este artigo é do Uber Engineering. Ele foi escrito por Chunyuan Li, Rosanne Liu e Jason Yosinski. A tradução foi feita pela Redação iMasters com autorização. Você pode conferir o original em: https://eng.uber.com/intrinsic-dimension/