Da última vez, sugeri sobre o uso de sequências De Bruijn para acelerar a iteração de conjuntos de bits. É um velho truque que (eu acho) foi descoberto por programadores de xadrez em nos anos 60 (eu realmente preciso de uma referência para isso).

É um clássico que gera um código elegante e quintessencial, mas realmente precisa de uma explicação paralela do que está acontecendo.

O problema

Para um número binário, escreva uma função que determina o número zeros perdidos, ou seja, quantas vezes você pode dividir esse número por 2 sem resto.

A implementação trivial é esta:

let rec ntz n =
    let rec loop acc n =
      if n land 1 = 1
      then acc
      else loop (acc+1) (n lsr 1)
    loop 0 n

É surpreendente saber que é possível encontrar a resposta sem fazer loop.

O menos importante

Se você observar o problema, rapidamente vai perceber que não há apenas um 1 que importa. O menos significativo.

Ele pode ser isolado da seguinte forma:

lso = n land ((lnot n) + 1)

ou (menor)

lso = n land (-n)

Vejamos alguns exemplos de números de tamanhos de byte

n	bin(n)	bin (lnot n)	bin (-n)	lso
2	0000 0010	1111 1101	1111 1110	0000 0010
7	0000 0111	1111 1000	1111 1001	0000 0001
40	0010 1000	1101 0111	1101 1000	0000 1000
48	0011 0000	1100 1111	1101 0000	0001 0000

Vamos fazer uma volta agora com teoria dos gráficos.

Gráficos De Bruijn

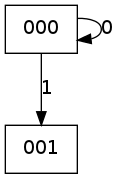
A coisa importante para lembrar é como você constrói esse gráfico. O exemplo a seguir é um gráfico de (2,3). Você começa com um vértice 000. Então, a partir de um vértice, você desloca ou um 1 ou um 0, e desenha uma borda para o nó de resultado. Itere e pare quando você tiver todos eles.

Assim, após a primeira etapa, você tem isto:

 

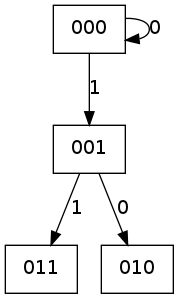
E no próximo passo você tem

 

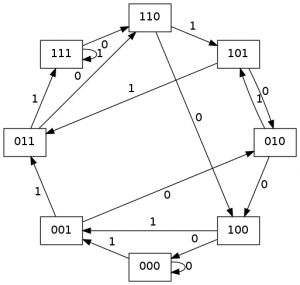
E o gráfico fechado é:

 

Sequências De Bruijn

A sequência De Bruijn é apenas um atalho para um caminho Hamiltionian (um caminho que visita cada vértice de uma vez) por meio de um gráfico De Bruijn. Um exemplo desse um caminho para o gráfico completo acima é:

000 -> 001 -> 010 -> 101 -> 011 -> 111 -> 110 -> 100 -> 000

Uma representação compacta para esse caminho pode ser gravada anotando o ponto de partida e as escolhas feitas em cada ponto. O exemplo produz a seguinte sequência:

00010111

Ao deslizar pela sequência, um bit por vez com uma janela de 3 bits, cada uma das oito possíveis sequências de três dígitos aparece exatamente uma vez.

n	index
000	0
001	1
010	2
011	4
100	7
101	3
110	6
111	5

O truque

A tabela acima mostra que em cada nó a quantos passos você está da fonte do gráfico. Então, se você multiplicar a sequência com o least significant one ou o nosso número, podemos usar a tabela para saber quantas trocas tivemos.

Por exemplo: 00010111 * 0010000 = 00101110000. Você mantém a sequência de 8 bits 0111000 que está mais à direita.

Ao olhar para a sequência de 3 (= 8-5) bits 011 da extrema esquerda, que você encontra deslocando cinco posições para a direita, você vê que eles estão no índice 4 na tabela. Portanto, o número tem 4 zeros à direita.

Resumo

Para encontrar o número de zeros perdidos para um número de 8 bits, você precisa

1. De uma sequência De Bruijn de 8 bits: debruijn = 00010111
2. De uma tabela de 8 entradas pré-computadas 0,1,2,4,7,3,6,5
3. Da seguinte fórmula:

lso = n & (-n)
ntz = table[(lso * debruijn) >> 5]

Versão de 64 bits

Se você quiser fazer isso para 64 bits, você tem que seguir exatamente o mesmo raciocínio. Você precisa de uma sequência debruijn de 64 bits (há 2^26 delas), e uma tabela pré-computada de tamanho 64.

#define DEBRUIJN 0x22fdd63cc95386dULL
static uint32_t table [64] ;
void inittable (){
    uint64_t db = DEBRUIJN ;
    int i ;
    for (i=0 ; i < 64;++ i ) {
        table [db >> 58] = i ;
        db = db <<1;
    }
}

uint32_t ntz ( uint64_t n){
    n &= −n ;
    n ∗= DEBRUIJN ;
    n >>= 58;
    return table [n] ;
}

Utilização em bitsets

Suponha que você esteja representando um bitset como um array de palavras de 64 bits. Ao iterar, você desliza através das palavras, e se um bit é 1 você faz a sua coisa. Se o resto das palavras através das quais você está deslizando contém apenas zeros, você está desperdiçando esforço. Conhecer o número de zeros perdidos permite calcular o último índice para o loop sobre os bits de uma palavra.

Um olhar sobre uma biblioteca padrão aleatória

Java

Existe uma classe java.util.BitSet que tem estado na biblioteca padrão java desde a versão 1.0. Já que o código é aberto, podemos inspecioná-lo. Vamos dar uma olhada.

O iterador usa

Long.numberOfTrailingZeros(word)

e a implementação é:

public static int numberOfTrailingZeros(long i) {
           // HD, Figure 5-14
           int x, y;
           if (i == 0) return 64;
           int n = 63;
           y = (int)i; if (y != 0) { n = n -32; x = y; } else x = (int)(i>>>32);
           y = x <<16; if (y != 0) { n = n -16; x = y; }
           y = x << 8; if (y != 0) { n = n - 8; x = y; }
           y = x << 4; if (y != 0) { n = n - 4; x = y; }
           y = x << 2; if (y != 0) { n = n - 2; x = y; }
           return n - ((x << 1) >>> 31);
}

 

(você pode ler o código fonte completo aqui: Long.java)

Se divirta!

***

Texto original disponível em http://blog.incubaid.com/2012/01/24/number-of-trailing-zeroes/